Question

【题目】某校260名学生参加植树活动，要求每人植4﹣7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵，将这四类的人数绘制成扇形图（如图1）和条形图（如图2）．

经确认扇形图是正确的，而条形图尚有一处错误．

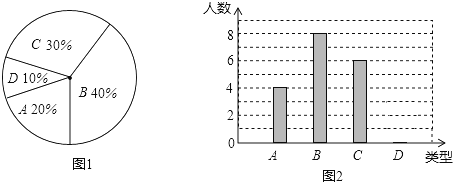
回答下列问题：

（1）写出条形图中存在的错误为________；

（2）写出这20名学生每人植树量的众数为________；中位数为________；

（3）经计算这20名学生每人植树量的平均数为5.3，则估算这260名学生共植树________棵；

（4）在这次活动中，九（1）班学生平均每人植6棵树，如果单独由男同学完成，每人应植树15棵，求如果单独由女同学完成，每人应植树多少棵？

Answer 1

【答案】（1）D；（2）5棵，5棵；（3）1378；（4）10棵.

【解析】试题分析：(1)、根据题意可得：D的人数为2，故D错误；(2)、根据众数和中位数的定义分别求出已知数据的众数和中位数；(3)、利用总人数乘以平均数得出答案；(4)、首先单独由女生完成，每人应植树x棵，然后根据题意列出分式方程，从而求出x的值得出答案．

试题解析：解：(1)、D错误，理由为：20×10%=2（人），

如图所示：

(2)、众数为，中位数为5棵；

(3)、估计260名学生共植树5.3×260=1378（棵）；

(4)、设单独由女生完成，每人应植树x棵，根据题意可得： ，

解得：x=10，经检验：x=10是原方程的解，即单独由女生完成，每人应植树10棵．