题目内容
4.|1-$\sqrt{2}$|+($\sqrt{5}-π$)0+($\frac{3}{7}$)-1+$\root{3}{-\frac{8}{27}}$×$\sqrt{\frac{49}{4}}$=$\sqrt{2}$.分析 原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算,最后一项利用平方根及立方根定义计算即可得到结果.
解答 解:原式=$\sqrt{2}$-1+1+$\frac{7}{3}$-$\frac{2}{3}$×$\frac{7}{2}$
=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.下列命题中的假命题是( )
| A. | 等腰三角形的顶角一定是锐角 | |
| B. | 等腰三角形的底角一定是锐角 | |
| C. | 等腰三角形至少有两个角相等 | |
| D. | 等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合 |
12.下列命题:
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
①两点确定一条直线;②两点之间,线段最短;③对顶角相等;④内错角相等;
其中真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.分式$\frac{1}{3{a}^{2}b}$与$\frac{1}{8a{b}^{2}}$的最简公分母是( )
| A. | 24a2b2 | B. | 24a3b3 | C. | 24a3b2 | D. | 24a2b3 |
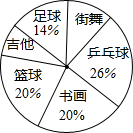 九(1)班全体同学根据自己的爱好参加了六个兴趣小组(每个学生必须参加且只参加一个),为了了解学生参加兴趣小组的情况,班主任参加各个兴趣小组的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“足球”小组的学生有7人,请解答下列问题:
九(1)班全体同学根据自己的爱好参加了六个兴趣小组(每个学生必须参加且只参加一个),为了了解学生参加兴趣小组的情况,班主任参加各个兴趣小组的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“足球”小组的学生有7人,请解答下列问题: