题目内容
如图,⊙O的半径是| 5 |
 的点称为格点.
的点称为格点.(1)写出⊙O上所有格点的坐标:
(2)设l为经过⊙O上任意两个格点的直线.
①满足条件的直线l共有多少条?
②求直线l同时经过第一、二、四象限的概率.
分析:(1)将点到圆心的距离小于等于
的横坐标、纵坐标都是整数的点求出即可;
(2)运用概率可将满足条件的直线条数求出;根据直线l同时经过第一、二、四象限的可能条数除以总的直线条数,即为直线l同时经过第一、二、四象限的概率.
| 5 |
(2)运用概率可将满足条件的直线条数求出;根据直线l同时经过第一、二、四象限的可能条数除以总的直线条数,即为直线l同时经过第一、二、四象限的概率.
解答:解:(1)格点坐标为:(1,2)、(1,-2)、(-1,2)、(-1,-2)、(2,1)、(2,-1)、(-2,1)、(-2,-1)
(2)①满足条件的直线l共有8×7÷2=28条
②“直线l同时经过第一、二、四象限”记为事件A,它的发生有4种可能,所有事件A发生的概率P(A)=
=
,即直线l同时经过第一、二、四象限的概率为
.
(2)①满足条件的直线l共有8×7÷2=28条
②“直线l同时经过第一、二、四象限”记为事件A,它的发生有4种可能,所有事件A发生的概率P(A)=
| 4 |
| 28 |
| 1 |
| 7 |
| 1 |
| 7 |
点评:此题为一次函数与概率的综合,考查的是用列表法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
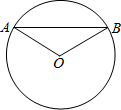 如图,⊙O的半径是4,∠AOB=120°,弦AB的长是
如图,⊙O的半径是4,∠AOB=120°,弦AB的长是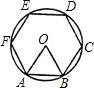 如图,⊙O的半径是6,求⊙O的内接正六边形ABCDEF的一边AB所对弧
如图,⊙O的半径是6,求⊙O的内接正六边形ABCDEF的一边AB所对弧
 如图,⊙O的半径是5,P是⊙O外一点,PO=8,∠OPA=30°,求AB和PB的长.
如图,⊙O的半径是5,P是⊙O外一点,PO=8,∠OPA=30°,求AB和PB的长.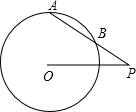 如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30°,则AB=
如图,⊙O的半径是5cm,P是⊙O外一点,PO=8cm,∠P=30°,则AB=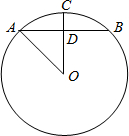 如图,⊙O的半径是10cm,弦AB的长是12cm,OC是⊙O的半径且OC⊥AB,垂足为D,则CD=
如图,⊙O的半径是10cm,弦AB的长是12cm,OC是⊙O的半径且OC⊥AB,垂足为D,则CD=