题目内容
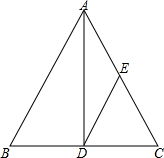 如图,等腰△ABC中,AB=AC,AD平分∠BAC,已知AD=BC=4,且△ADE的面积等于△CDE,求DE的长度.
如图,等腰△ABC中,AB=AC,AD平分∠BAC,已知AD=BC=4,且△ADE的面积等于△CDE,求DE的长度.考点:直角三角形斜边上的中线,等腰三角形的性质,勾股定理
专题:
分析:根据等腰三角形三线合一的性质可得AD⊥C,BD=CD,再根据等底等高的三角形的面积相等求出AE=CE,再利用勾股定理列式求出AB,然后根据直角三角形斜边上的中线等于斜边的一半可得DE=
AC.
| 1 |
| 2 |
解答:
解:∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD=
BC=
×4=2,
∵△ADE的面积等于△CDE,
∴AE=CE,
在Rt△ABD中,由勾股定理得,AB=
=
=2
,
∴AC=AB=2
,
∴DE=
AC=
.
∴AD⊥BC,BD=CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ADE的面积等于△CDE,
∴AE=CE,
在Rt△ABD中,由勾股定理得,AB=
| AD2+BD2 |
| 42+22 |
| 5 |
∴AC=AB=2
| 5 |
∴DE=
| 1 |
| 2 |
| 5 |
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理,熟记性质与定理是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 | ||
B、一次抽奖活动中,“中奖的概率是
| ||
| C、“明天降雨的概率是86%”表示明天有86%的时间降雨 | ||
| D、“刘明夺冠的可能性是98%”表示刘明夺冠的可能性很大 |
若把分式
中的x和y都扩大2倍,那么分式的值( )
| x+y |
| 3x |
| A、扩大2倍 | B、不变 |
| C、缩小2倍 | D、缩小4倍 |
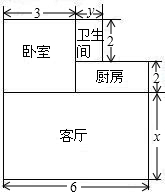 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: 阅读材料:
阅读材料: