题目内容
已知含字母a,b的代数式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)
(1)化简代数式;
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少?
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?
【考点】整式的加减—化简求值.
【专题】计算题;整式.
【分析】(1)原式去括号合并即可得到结果;
(2)由a与b互为倒数得到ab=1,代入(1)结果中计算求出b的值即可;
(3)根据(1)的结果确定出b的值即可.
【解答】解:(1)原式=3a2+6b2+6ab﹣12﹣3a2﹣6b2﹣4ab+4a+4=2a b+4a﹣8;
b+4a﹣8;
(2)∵a,b互为倒数,
∴ab=1,
∴2+4a﹣8=0,
解得:a=1.5,
∴b= ;
;
(3)由(1)得:原式=2ab+4a﹣8=(2b+4)a﹣8,
由结果与a的值无关,得到2b+4=0,
解得:b=﹣2.
【点评】此题考查了整式的加减﹣化简求值,倒数,熟练掌握运算法则是解本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
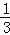 .
.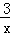 ,x+y,x2+y2,﹣3,
,x+y,x2+y2,﹣3,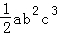 中,单项式共有( )
中,单项式共有( )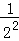 =1﹣
=1﹣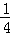 =
=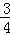 =
=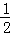 ×
×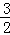
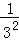 =1﹣
=1﹣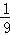 =
=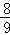 =
=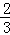 ×
×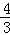
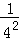 =1﹣
=1﹣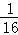 =
=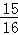 =
= ×
×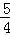
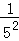 =1﹣
=1﹣ =
=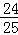 =
=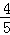 ×
×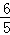 …
…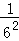 =__________×__________; 1﹣
=__________×__________; 1﹣ =__________×__________;
=__________×__________;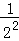 )×(1﹣
)×(1﹣ )×(1﹣
)×(1﹣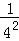 )×…×(1﹣
)×…×(1﹣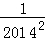 )×(1﹣
)×(1﹣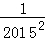 ).
).