题目内容
⊙O中，∠AOB=100°，若C是
上一点，则∠ACB等于
- A.80°
- B.100°
- C.120°
- D.130°
D
分析：首先根据题意画出图形，然后在优弧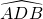
上取点D，连接AD，BD，由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠ADB的度数，又由圆的内接四边形的对角互补，即可求得∠ACB的度数．
解答：
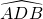解：如图：在优弧上取点D，连接AD，BD，
∵⊙O中，∠AOB=100°，
∴∠ADB=
∠AOB=50°，
∵四边形ACBD是⊙O的内接四边形，
∴∠ACB=180°-∠ADB=130°．
故选D．
点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，解题的关键是利用数形结合思想解题，注意辅助线的作法．
分析：首先根据题意画出图形，然后在优弧
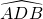上取点D，连接AD，BD，由在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半，即可求得∠ADB的度数，又由圆的内接四边形的对角互补，即可求得∠ACB的度数．解答：
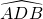解：如图：在优弧上取点D，连接AD，BD，∵⊙O中，∠AOB=100°，
∴∠ADB=
∠AOB=50°，∵四边形ACBD是⊙O的内接四边形，
∴∠ACB=180°-∠ADB=130°．
故选D．
点评：此题考查了圆周角定理与圆的内接四边形的性质．此题难度不大，解题的关键是利用数形结合思想解题，注意辅助线的作法．
练习册系列答案
相关题目
31、如图，已知扇形OACB中，∠AOB=120°，弧AB长为L=4π，⊙O′和弧AB，OA，OB分别相切于点C，D，E，求⊙O的周长．
如图，⊙O中，∠AOB=110°，点C、D是
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．（直接填写答案）