题目内容
如图，关于∠α与∠β的同一种三角函数值，有三个结论：①tanα＞tanβ，②sinα＞sinβ，③cosα＞cosβ．正确的结论为
- A.①②
- B.②③
- C.①③
- D.①②③
A
分析：首先根据图形可得：∠α＞∠β，然后根据各锐角函数的增减性，即可求得答案．
解答：根据图形得：∠α＞∠β，
∴tanα＞tanβ，sinα＞sinβ，cosα＜cosβ．
∴①②正确．
故选A．
点评：此题考查了锐角函数的增减性与三角形外角的性质．注意当角度在0°～90°间变化时，
①正弦值随着角度的增大（或减小）而增大（或减小）；
②余弦值随着角度的增大（或减小）而减小（或增大）；
③正切值随着角度的增大（或减小）而增大（或减小）．
分析：首先根据图形可得：∠α＞∠β，然后根据各锐角函数的增减性，即可求得答案．
解答：根据图形得：∠α＞∠β，
∴tanα＞tanβ，sinα＞sinβ，cosα＜cosβ．
∴①②正确．
故选A．
点评：此题考查了锐角函数的增减性与三角形外角的性质．注意当角度在0°～90°间变化时，
①正弦值随着角度的增大（或减小）而增大（或减小）；
②余弦值随着角度的增大（或减小）而减小（或增大）；
③正切值随着角度的增大（或减小）而增大（或减小）．
练习册系列答案
相关题目
19、如图，关于直线l对称的两个圆的半径都为1，等边三角形ABC，LMN的顶点分别在两圆上，AB⊥l，MN∥l，将l左侧的图形进行平移、旋转或翻折变换（以下所述“变换”均值这3种变换之一），可以与l右侧的图形重合．
设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
所以，当r＜a时，⊙O与正方形的公共点的个数可能有 个；
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：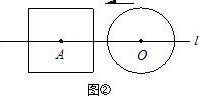
所以，当r=a时，⊙O与正方形的公共点个数可能有 个；
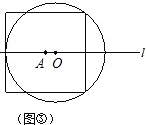
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
a；
（4）就r＞a的情形，请你仿照“当…时，⊙O与正方形的公共点个数可能有 个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a+r | |
d=a+r |
|
| a≤d＜a+r | |
| d=a-r | |
| d＜a-r |
（2）如图②，当r=a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：
| d、a、r之间关系 | 公共点的个数 |
| d＞a+r | |
| d=a+r | |
| a≤d＜a+r | |
| d＜a |
（3）如图③，当⊙O与正方形有5个公共点时，试说明r=
| 5 |
| 4 |
（4）就r＞a的情形，请你仿照“当…时，⊙O与正方形的公共点个数可能有
（注：第（4）小题若多给出一个正确结论，则可多得2分，但本大题得分总和不得超过12分）．
（2013•龙湾区一模）如图，Rt△ABE与Rt△DCF关于直线m对称，若∠B=90°，∠C=90°，连结EF，AD，点B，E，F，C在同一条直线上．求证：四边形ABCD是矩形．
如图，正方形ABCD与正方形A′B′C′D′关于点O中心对称，若正方形ABCD的边长为1，设图形重合部分的面积为y，线段OB的长为x，求y与x之间的函数关系式．