题目内容
已知点A为函数 在第一象限内的点,且A点的纵坐标是横坐标的
在第一象限内的点,且A点的纵坐标是横坐标的 倍.
倍.(1)求点A的坐标,
(2)点B为y轴正半轴上的一点,且OB=OA,求经过A、B两点的一次函数关系式.
【答案】分析:(1)首先根据题意设A(a, ),把A点坐标代入y=
),把A点坐标代入y= 中,可求出A点坐标;
中,可求出A点坐标;
(2)根据题意利用勾股定理求出OA的长,从而求得B点坐标,再把A,B点的坐标代入一次函数解析式,利用待定系数法求出答案.
解答:解:(1)∵A点的纵坐标是横坐标的 倍.
倍.
∴设A(a, ),
),
∵点A在函数 的图象上,
的图象上,
∴a• a=12,
a=12,
解得:a=±3,
∵点A为函数 在第一象限内的点,
在第一象限内的点,
∴点A的坐标是(3,4);
(2)OA= =5,
=5,
∵OA=OB,且点B为y轴正半轴上,
∴B(0,5),
设一次函数解析式为:y=kx+b,
∴ ,
,
解得: ,
,
∴经过A、B两点的一次函数关系式为:y=- x+5.
x+5.
点评:此题主要考查了反比例函数图象上点的坐标特点,以及利用待定系数法求函数解析式,关键把握两点:①所有在反比例函数上的点的横纵坐标的积应等于比例系数,②凡是图象过的点都能满足关系式.
 ),把A点坐标代入y=
),把A点坐标代入y= 中,可求出A点坐标;
中,可求出A点坐标;(2)根据题意利用勾股定理求出OA的长,从而求得B点坐标,再把A,B点的坐标代入一次函数解析式,利用待定系数法求出答案.
解答:解:(1)∵A点的纵坐标是横坐标的
 倍.
倍.∴设A(a,
 ),
),∵点A在函数
 的图象上,
的图象上,∴a•
 a=12,
a=12,解得:a=±3,
∵点A为函数
 在第一象限内的点,
在第一象限内的点,∴点A的坐标是(3,4);
(2)OA=
 =5,
=5,∵OA=OB,且点B为y轴正半轴上,
∴B(0,5),
设一次函数解析式为:y=kx+b,
∴
 ,
,解得:
 ,
,∴经过A、B两点的一次函数关系式为:y=-
 x+5.
x+5.点评:此题主要考查了反比例函数图象上点的坐标特点,以及利用待定系数法求函数解析式,关键把握两点:①所有在反比例函数上的点的横纵坐标的积应等于比例系数,②凡是图象过的点都能满足关系式.

练习册系列答案
相关题目
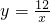 在第一象限内的点,且A点的纵坐标是横坐标的
在第一象限内的点,且A点的纵坐标是横坐标的 倍.
倍. 在第一象限内的点,且A点的纵坐标是横坐标的
在第一象限内的点,且A点的纵坐标是横坐标的 倍.
倍. 已知点A是双曲线
已知点A是双曲线 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为________.
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为________.