题目内容
1．已知a-b=2，b-c=-1，求a2+b2+c2-ab-bc-ca的值．分析 首先由a-b=3，b-c=-1，求得a-c=2，再将a2+b2+c2-ab-bc-ca变形为$\frac{1}{2}$（2a2+2b2+2c2-2ab-2bc-2ca），即得$\frac{1}{2}$[（a-b）2+（a-c）2+（b-c）2]，代入求值即可．
解答 解：原式=$\frac{1}{2}$（2a2+2b2+2c2-2ab-2bc-2ac）
=$\frac{1}{2}$[（a-b）2+（a-c）2+（b-c）2]
∵a-b=2，b-c=-1，
∴a-c=1，
∴原式=$\frac{1}{2}$×[22+12+（-1）2]=3．
点评 此题考查了利用完全平方公式因式分解的应用．注意整体思想的渗透，将原式变形为完全平方式的和是解题的关键．
练习册系列答案
相关题目
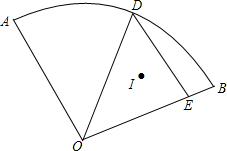如图所示扇形AOB中，∠AOB=90°，OA=OB=6，D为弧上一动点，过D作DE∥OA交OB于点E．I为△ODE的内心，当点D运动时，I也随着运动．则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$．
10．
如图，有一块形如等腰直角三角形的木板，直角边长为a，要用它截出一块矩形木板DEFG，则矩形木板DEFG的面积不可能是（ ）
如图，有一块形如等腰直角三角形的木板，直角边长为a，要用它截出一块矩形木板DEFG，则矩形木板DEFG的面积不可能是（ ）| A． | $\frac{{a}^{2}}{6}$ | B． | $\frac{{a}^{2}}{5}$ | C． | $\frac{{a}^{2}}{4}$ | D． | $\frac{{a}^{2}}{3}$ |
已知a，b，c在数轴上对应的点的位置如图所示：化简：|b+c|+|a+c|-|b-a|-|a+b+c|．