题目内容
7．
如图，BD和CE是△ABC的角平分线．∠1=25°，∠2=20°，求∠A．
分析 根据角平分线的定义可求出∠ABC和∠ACB的度数，然后在△ABC中运用三角形内角和定理可求出∠A．
解答 解：∵BD和CE是△ABC的角平分线，∠1=25°，∠2=20°，
∴∠1=$\frac{1}{2}$∠ABC=25°，∠2=$\frac{1}{2}$∠ACB=20°，
∴∠ABC=50°，∠ACB=40°，
∴∠A=180°-50°-40°=90°．
点评 本题主要考查了角平分线的定义、三角形内角和定理等知识，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
17．-（-9）的相反数是（ ）
| A． | 9 | B． | -9 | C． | $\frac{1}{9}$ | D． | -$\frac{1}{9}$ |
18．在时刻8：40，时钟上的时针和分针之间的夹角为（ ）
| A． | 15° | B． | 20° | C． | 25° | D． | 10° |
15．某商品按进价的100%加价出售，经过一段时间，商家为减少库存，决定以7折销售，这时每件商品（ ）
| A． | 赚40% | B． | 赔30% | C． | 赔40% | D． | 不赔不赚 |
2．
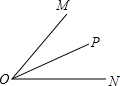已知，如图，OP平分∠MON，则下列式子中错误的是（ ）
已知，如图，OP平分∠MON，则下列式子中错误的是（ ）| A． | ∠MOP=∠NOP | B． | ∠MOP=$\frac{1}{2}$∠MON | C． | ∠MON=2∠NOP | D． | ∠MOP+∠NOP＞∠MON |
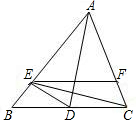如图，AD是角平分线，E是AB上一点，AE=AC，EF∥BC交AC于F．下列结论①△ADC≌△ADE；②CE平分∠DEF；③AD垂直平分CE．其中正确的是①②③（填序号）．
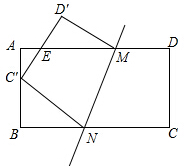如图，把矩形纸片ABCD折叠，使点C落在AB边上的点C′处（与点A，B不重合），点D落在D′处，C′D′交AD于点E，折痕为MN．
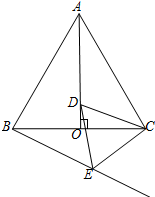如图，AO是边长为2的等边△ABC的高，点D是AO上的一个动点（点D不与点A、O重合），以CD为一边在AC下方作等边△CDE，连结BE并延长，交AC的延长线于点F．
已知：如图，点M在锐角∠AOB的内部，在OA边上求作一点P，在OB边上求作一点Q，使得MP+PQ最小．若OM=2，OM平分∠AOB，并且∠AOB=20°，求这个最小值．