��Ŀ����
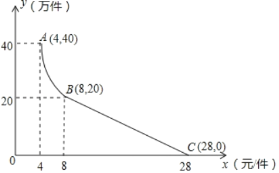
����Ŀ��ij�Ƽ�����˾��160��Ԫ��Ϊ�²�Ʒ���з����ã��ɹ����Ƴ���һ���г�����ĵ��Ӳ�Ʒ�����ڵ���Ͷ���������������ۣ���֪�������ֵ��Ӳ�Ʒ�ijɱ�Ϊ4Ԫ/���������۹����з��֣�ÿ�����������y������������ۼ۸�x��Ԫ/�����Ĺ�ϵ��ͼ��ʾ������ABΪ����������ͼ���һ���֣��蹫˾�������ֵ��Ӳ�Ʒ��������Ϊs����Ԫ������ע������һ��ӯ������ӯ����������һ�������������һ���������������һ��ijɱ���
��1�������y���������x��Ԫ/�����ĺ�������ʽ��
��2�������һ�����ֵ��Ӳ�Ʒ��������s����Ԫ����x��Ԫ/�����ĺ�������ʽ���������һ������������ֵ��
��3�����蹫˾�����ֵ��Ӳ�Ʒ��һ��ǡ�ð�������s����Ԫ��ȡ�����ֵʱ�������ۣ��ָ��ݵ�һ���ӯ������������ڶ������ֵ��Ӳ�Ʒÿ�������ۼ۸�x��Ԫ/��������8Ԫ���ϣ�x��8�������ڶ������������103��Ԫʱ������������s����Ԫ�������ۼ۸�x��Ԫ/�����ĺ���ʾ��ͼ�������ۼ۸�x��Ԫ/������ȡֵ��Χ��
���𰸡���1��y�� ����2��s������x��16��2��16����ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ����3��11��x��21
����2��s������x��16��2��16����ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ����3��11��x��21
��������
��1�����ݴ���ϵ�������������y���������x��Ԫ/����֮��ĺ�����ϵʽ��
��2������������������ۣ���x=8ʱ��smax=-80����x=16ʱ��smax=-16������-16��-80���ɵõ�ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ-16��Ԫ��
��3�����ݵڶ����������s=��x-4����-x+28��-16=-x2+32x-128����s=103���ɵ÷���103=-x2+32x-128�����x1=11��x2=21��Ȼ����ƽ��ֱ������ϵ�У�����s��x�ĺ���ͼ����ͼ�ɵó����ۼ۸�x��Ԫ/������ȡֵ��Χ��
�⣺��1����4��x��8ʱ����y��![]() ����A��4��40�������k��4��40��160��
����A��4��40�������k��4��40��160��
��y��x֮��ĺ�����ϵʽΪy��![]() ��
��
��8��x��28ʱ����y��k'x+b����B��8��20����C��28��0������ã�
![]() �����
�����![]() ��
��
��y��x֮��ĺ�����ϵʽΪy����x+28��
����������y�� ��
��
��2����4��x��8ʱ��s����x��4��y��160����x��4��![]() ��160����
��160����![]() ��
��
�ߵ�4��x��8ʱ��s����x�����������
�൱x��8ʱ��smax����![]() ����80��
����80��
��8��x��28ʱ��s����x��4��y��160����x��4������x+28����160������x��16��2��16��
�൱x��16ʱ��smax����16��
�ߩ�16����80��
�൱ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ��
��3���ߵ�һ���������Ϊ��16��Ԫ��
��16��ԪӦ��Ϊ�ڶ���ijɱ���
�֡�x��8��
��ڶ����������s����x��4������x+28����16����x2+32x��128��
��s��103����103����x2+32x��128��
���x1��11��x2��21��
��ƽ��ֱ������ϵ�У�����s��x�ĺ���ʾ��ͼ�ɵã�

�۲�ʾ��ͼ��֪����s��103
�൱11��x��21ʱ���ڶ����������s������103��Ԫ��

����Ŀ������ij��˾�����βɹ���һ��ԭ�ϣ���֪�ڶ��εIJɹ������ǵ�һ�βɹ�������������������Ϣ���±���
��һ�� | �ڶ��� | |
ÿ��ԭ�ϵļ۸�Ԫ�� | m+500 | m-500 |
�ɹ����ã���Ԫ�� | 40 | 60 |
��1����m��ֵ������������ι��ɹ��˶��ٶ�ԭ�ϣ�
��2���ù�˾�ɽ�ԭ�ϼӹ���A�Ͳ�Ʒ��B�Ͳ�Ʒ�������豸����ÿ��ֻ�ܰ��żӹ�һ���ͺŲ�Ʒ����ͳ�ƣ��ӹ�A�Ͳ�Ʒ��B�Ͳ�Ʒ��1�칲����ԭ����Ϊ20�֣��ӹ�3��A�Ͳ�Ʒ��ӹ�2��B�Ͳ�Ʒ������ԭ������ȣ�������ӹ���A��B�Ͳ�Ʒÿ�������ԭ�����ֱ��Ƕ��ٶ֣�
��3���ù�˾�����������ֲ�Ʒȫ�����ڹ��⣬ÿ��ԭ�ϼӹ���A��B�Ͳ�Ʒ��Ļ����ֱ���1000Ԫ��600Ԫ����Ҫ��ӹ�ʱ�䲻����30�죮Ϊ��ʹ�����������Ӧ���������ļӹ�������
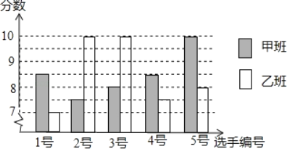
����Ŀ���й����õĿ��ٷ�չ���ڶ���Ҹ��ܵ�����в�����ŵ��㵺�¼����Ϻ�Σ���������뺫��ϵ���¼��ķ��������Ұ�ȫһ���ܵ���в����ν������������ƥ����������ijУ������չ����֪ʶ���������꼶�ס�������ֱ�ѡ5��ͬѧ�μ�������֪ʶ����������Ԥ���ɼ���ͼ��ʾ��
��1��������ͼ��д�����
ƽ���� | ��λ�� | ���� | ���� | |
�װ� | 8.5 | 8.5 | ||
�Ұ� | 8.5 | 10 | 1.6 |
��2������������ݣ������ĸ���ijɼ��Ϻã�����ϸ˵����