题目内容
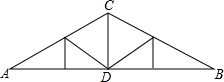如图所示，某厂车间的人字屋架为等腰三角形，跨度AB=12m，∠A=30°，求中柱CD和上弦AC的长．（结果保留根号，注：sin30°=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
考点：解直角三角形的应用
专题：
分析：利用等腰三角形的性质结合锐角三角函数关系分别得出即可．
解答：解：由题意可得：∵AB=12m，∠A=30°，
∴AD=BD=6m，
∴tan30°=
，
∴CD=6tan30°=2
，
∵cos30°=
∴AC=
=4
．
答：中柱CD的长为2
m和上弦AC的长为4
m．
∴AD=BD=6m，
∴tan30°=
| CD |
| AD |
∴CD=6tan30°=2
| 3 |
∵cos30°=
| AD |
| AC |
∴AC=
| 6 |
| cos30° |
| 3 |
答：中柱CD的长为2
| 3 |
| 3 |
点评：此题主要考查了解直角三角形的应用，熟练应用锐角三角函数关系是解题关键．
练习册系列答案
相关题目
在△ABC和△EMN中，已知∠A=50°，∠B=60°，∠E=70°，∠M=60°，AC=EN，则这两个三角形（ ）
| A、一定全等 | B、一定不全等 |
| C、不一定全等 | D、以上都不对 |
计算（-3）×（4-12），用分配律计算过程正确的是（ ）
| A、（-3）×4+（-3）×（-12） |
| B、（-3）×4-（-3）×（-12） |
| C、3×4-（-3）×（-12） |
| D、（-3）×4+3×（-12） |
