题目内容
(1)如图1,直线AB、CD相交于点O,FO⊥CD于点O,且∠EOF=∠DOB.求∠EOB的度数.
(2)如图2,O为直线AB上一点,OD平分∠AOC,∠AOC=58°,∠DOE=90°.求∠BOE的度数.

(2)如图2,O为直线AB上一点,OD平分∠AOC,∠AOC=58°,∠DOE=90°.求∠BOE的度数.

考点:对顶角、邻补角,角平分线的定义,垂线
专题:几何图形问题
分析:(1)根据垂直的定义可以得到∠FOD=90°,即∠EOF+∠EOD=90°,然后根据∠EOF=∠DOB,即可求解;
(2)首先根据角平分线的定义求得∠AOD的度数,即可求得∠AOE的度数,则∠BOE即可求解.
(2)首先根据角平分线的定义求得∠AOD的度数,即可求得∠AOE的度数,则∠BOE即可求解.
解答:解:(1)∵FO⊥CD,
∴∠FOD=90°,即∠EOF+∠EOD=90°,
∵∠EOF=∠DOB,
∴∠DOB+∠EOD=90°,
即∠EOB=90°;
(2)∵OD平分∠AOC,
∴∠AOD=
∠AOC=
×58°=29°,
∵∠AOB=180°,∠DOE=90°,
∴∠BOE=180°-90°-29°=61°.
∴∠FOD=90°,即∠EOF+∠EOD=90°,
∵∠EOF=∠DOB,
∴∠DOB+∠EOD=90°,
即∠EOB=90°;
(2)∵OD平分∠AOC,
∴∠AOD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=180°,∠DOE=90°,
∴∠BOE=180°-90°-29°=61°.
点评:本题考查对顶角的性质以及邻补角的定义和垂直的定义,是一个需要熟记的内容.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
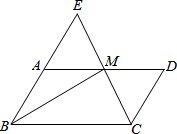 已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:
已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证: