题目内容
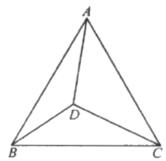
【题目】如图,在△ABC中,![]() ,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
(1)求线段BC的长;
(2)①当点D与点A、点C不重合时,过点D作DE⊥AB于点E,DF⊥BC于点F,连接ME,MF,在射线BD旋转的过程中,∠EMF的大小是否发生变化?若不变,求∠EMF的度数;若变化,请说明理由.
②在①的条件下,连接EF,直接写出△EFM面积的最小值______.
【答案】(1)![]() ;(2)不变,90°;(3)
;(2)不变,90°;(3)![]() .
.
【解析】
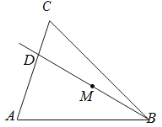
(1)如图1中,作![]() 于
于![]() .解直角三角形求出
.解直角三角形求出![]() ,证明
,证明![]() 是等腰直角三角形即可解决问题.
是等腰直角三角形即可解决问题.
(2)①利用直角三角形斜边中线定理,证明![]() 是等腰直角三角形即可解决问题.
是等腰直角三角形即可解决问题.
②如图2中,由①可知![]() 是等腰直角三角形,当
是等腰直角三角形,当![]() 的值最小时,
的值最小时,![]() 的面积最小,因为
的面积最小,因为![]() ,推出当
,推出当![]() 时,
时,![]() 的值最小,此时
的值最小,此时![]() .
.
解:(1)如图1中,作![]() 于
于![]() .
.
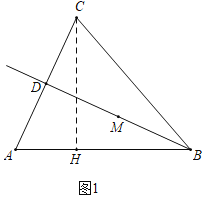
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)①结论:![]() 不变.
不变.
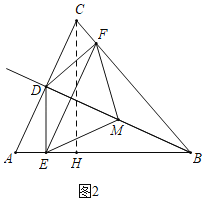
理由:如图2中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
②如图2中,作![]() 于
于![]() ,由①可知
,由①可知![]() 是等腰直角三角形,
是等腰直角三角形,
![]() 当
当![]() 的值最小时,
的值最小时,![]() 的面积最小,
的面积最小,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 的值最小,此时
的值最小,此时![]() ,
,
![]() 的最小值
的最小值![]() ,
,
![]() 的面积的最小值
的面积的最小值![]() .
.
故答案为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目