题目内容
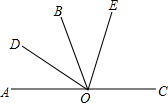 如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.
如图,O在直线AC上,OD是∠AOB的平分线,OE在∠BOC内.(1)若OE是∠BOC的平分线,则有OD⊥OE,试说明理由;
(2)若∠BOE=
| 1 |
| 2 |
考点:角平分线的定义
专题:
分析:(1)根据角平分线的定义可以求得∠DOE=
∠AOC=90°;
(2)设∠EOB=x度,∠EOC=2x度,把角用未知数表示出来,建立x的方程,用代数方法解几何问题是一种常用的方法.
| 1 |
| 2 |
(2)设∠EOB=x度,∠EOC=2x度,把角用未知数表示出来,建立x的方程,用代数方法解几何问题是一种常用的方法.
解答: 解:(1)如图,∵OD是∠AOB的平分线,OE是∠BOC的平分线,
解:(1)如图,∵OD是∠AOB的平分线,OE是∠BOC的平分线,
∴∠BOD=
∠AOB,∠BOE=
∠BOC,
∴∠DOE=
(∠AOB+∠BOC)=
∠AOC=90°,即OD⊥OE;
(2)设∠EOB=x,则∠EOC=2x,
则∠BOD=
(180°-3x),
则∠BOE+∠BOD=∠DOE,
即x+
(180°-3x)=72°,
解得x=36°,
故∠EOC=2x=72°.
 解:(1)如图,∵OD是∠AOB的平分线,OE是∠BOC的平分线,
解:(1)如图,∵OD是∠AOB的平分线,OE是∠BOC的平分线,∴∠BOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
(2)设∠EOB=x,则∠EOC=2x,
则∠BOD=
| 1 |
| 2 |
则∠BOE+∠BOD=∠DOE,
即x+
| 1 |
| 2 |
解得x=36°,
故∠EOC=2x=72°.
点评:本题考查了角平分线的定义.设未知数,把角用未知数表示出来,列方程组,求解.角平分线的运用,为解此题起了一个过渡的作用.

练习册系列答案
相关题目
用12米长的铝材制成一个矩形窗框,使它的面积为6平方米,若设它的一条边长为x米,则根据题意可列出关于x的方程为( )
| A、x(6+x)=6 |
| B、x(6-x)=6 |
| C、x(12-x)=6 |
| D、x(12-2x)=6 |
下列各组中的两个图形,一定相似的是( )
| A、有一个角对应相等的两个菱形 |
| B、对应边成比例的两个多边形 |
| C、两条对角线对应成比例的两个平行四边形 |
| D、任意两个矩形 |
已知线段AB=8cm,在直线AB上有一点C,且BC=4cm,点M是线段AC的中点,则线段AM的长为( )
| A、2cm |
| B、4cm |
| C、2cm或6cm |
| D、4cm或6cm |
 有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )
有理数a、b在数轴上的位置如图所示,则下列各式中错误的是( )| A、b<0<a |
| B、|b|>|a| |
| C、a+b>0 |
| D、ab<0 |
 如图,BE是⊙O的直径,点A,C,D,F都在⊙O上,
如图,BE是⊙O的直径,点A,C,D,F都在⊙O上,
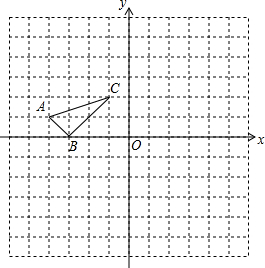 每个小正方形边长都为1个单位长度.
每个小正方形边长都为1个单位长度.