题目内容
 如图点M,N在反比例函数y=
如图点M,N在反比例函数y=| k | x |
说明:S△EFM=S△EFN.
分析:根据点M,N在反比例函数y=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,连接MO,NO,延长FN,作EA⊥FN于点A,得出△EFM与△EOM等底同高,△EFN与△FNO等底同高,进而得出S△EFM=S△FNO=
k,S△EMO=S△EFM=
k,得出答案即可.
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:连接MO,NO,延长FN,作EA⊥FN于点A,
证明:连接MO,NO,延长FN,作EA⊥FN于点A,
∵△EFM与△EOM等底同高,△EFN与△FNO等底同高,
∴S△EFM=S△FNO,S△EMO=S△EFM,
∵点M,N在反比例函数y=
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,
∴xy=k,
∴S△EFM=S△FNO=
k,S△EMO=S△EFM=
k,
∴S△EFM=S△EFN.
 证明:连接MO,NO,延长FN,作EA⊥FN于点A,
证明:连接MO,NO,延长FN,作EA⊥FN于点A,∵△EFM与△EOM等底同高,△EFN与△FNO等底同高,
∴S△EFM=S△FNO,S△EMO=S△EFM,
∵点M,N在反比例函数y=
| k |
| x |
∴xy=k,
∴S△EFM=S△FNO=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△EFM=S△EFN.
点评:此题主要考查了反比例函数的综合应用,根据已知得出△EFM与△EOM等底同高,△EFN与△FNO等底同高是解题关键.

练习册系列答案
相关题目
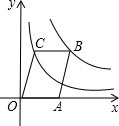 如图,B、C分别在反比例函数
如图,B、C分别在反比例函数
 与反比例函数
与反比例函数 的图象上,点A在x轴上,且四边形OABC是平行四边形,则四边形OABC的面积为 .
的图象上,点A在x轴上,且四边形OABC是平行四边形,则四边形OABC的面积为 .
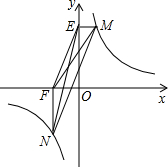 如图点M,N在反比例函数
如图点M,N在反比例函数 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.