题目内容
4.计算:(1)计算:(-$\frac{1}{2}$)-1-3tan30°+(1-$\sqrt{2}$)0+$\sqrt{12}$
(2)解方程:(x-2)2+x(x-2)=0.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、特殊角的三角函数值计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先把方程左边化为两个因式积的形式,再求出x的值即可.
解答 解:(1)原式=-2-3×$\frac{\sqrt{3}}{3}$+1+2$\sqrt{3}$
=-2-$\sqrt{3}$+1+2$\sqrt{3}$
=$\sqrt{3}$-1;
(2)∵原方程可化为(x-2)(2x-2)=0,
∴x-2=0或2x-2=0,
∴x1=2,x2=1.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的计算法则、特殊角的三角函数值是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列计算正确的是( )
| A. | a0=1 | B. | x2÷x3=$\frac{1}{x}$ | C. | (-$\frac{x}{y}$)2=-$\frac{{x}^{2}}{y}$ | D. | a4÷2-1=$\frac{1}{2}$a4 |
12.下列二次根式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{24}$ | C. | $\sqrt{48}$ | D. | $\sqrt{32}$ |
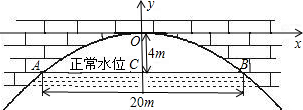 有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.
有座抛物线形拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m,为了保证过往船只顺利航行,桥下水面的宽度不得小于18m.