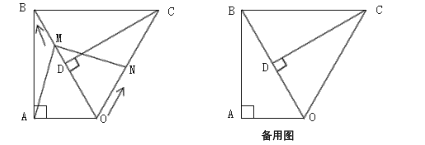
题目内容
【题目】如图1所示,在正方形ABCD和正方形![]() 中,
中,![]() ,连结
,连结![]() .
.
(1)问题发现:![]() _________;
_________;
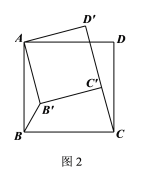
(2)拓展探究:将正方形![]() 绕点A逆时针旋转,记旋转角为
绕点A逆时针旋转,记旋转角为![]() ,连结
,连结![]() ,试判断:当
,试判断:当![]() ≤
≤![]()
![]() 时,
时,![]() 的值有无变化?请仅就图2中的情形给出你的证明;
的值有无变化?请仅就图2中的情形给出你的证明;
(3)问题解决:请直接写出在旋转过程中,当![]() 三点共线时
三点共线时![]() 的长.
的长.


【答案】(1)![]() ;(2)无变化,理由见解析;(3)
;(2)无变化,理由见解析;(3)![]() 的长为
的长为![]() 或
或![]()
【解析】
(1)延长![]() 交BC于点E,到等腰直角三角形,根据两直角边相等可得出结果
交BC于点E,到等腰直角三角形,根据两直角边相等可得出结果
(2) 先根据两个等腰直角三角形相似得出![]() ,根据这个条件可以得到△
,根据这个条件可以得到△![]() ∽△
∽△![]() ,就可以得出结论。
,就可以得出结论。
(3)![]() 共线分两种情况,根据旋转角度的不同进行分类讨论。
共线分两种情况,根据旋转角度的不同进行分类讨论。
(1)![]() ;
;
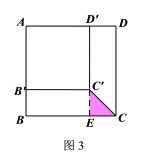
提示:延长![]() 交BC于点E,如图3所示.
交BC于点E,如图3所示.
则![]() ,△
,△![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∴![]() .
.
(2)无变化;
理由如下:连结AC、![]() ,如图4所示.
,如图4所示.
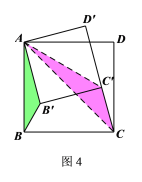
∵△ABC和△![]() 均为等腰直角三角形
均为等腰直角三角形
∴![]()
∵![]()
∴![]()
∴△![]() ∽△
∽△![]()
∴![]()
∴当![]() ≤
≤![]() <360°时,
<360°时,![]() 的值无变化;
的值无变化;
(3)![]() 的长为
的长为![]() 或
或![]() .
.
提示:分为两种情况:
①如图5所示,连结AC.
![]()
在Rt△![]() 中,由勾股定理得:
中,由勾股定理得:
![]()
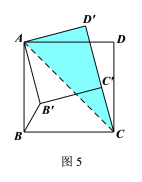
∴![]()
∵![]()
∴![]() ;
;
②如图6所示,
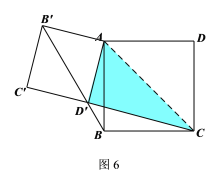
此时![]()
∵![]()
∴![]() .
.
综上所述,![]() 的长为
的长为![]() 或
或![]() .
.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目