题目内容
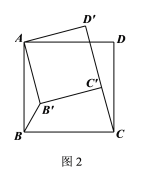
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,点
,点![]() 是点
是点![]() 以
以![]() 为对称中心的对称点,点
为对称中心的对称点,点![]() 运动的同时,点
运动的同时,点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,当点
,当点![]() 到达顶点
到达顶点![]() 时,
时,![]() 同时停止运动,设
同时停止运动,设![]() 两点运动时间为
两点运动时间为![]() 秒.
秒.
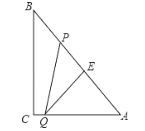
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)四边形![]() 面积能否是
面积能否是![]() 面积的
面积的![]() ?若能,求出此时
?若能,求出此时![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() 为等腰三角形?(直接写出结果)
为等腰三角形?(直接写出结果)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)能,
;(3)能,![]() ;(4)
;(4)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先在![]() 中,由勾股定理求出
中,由勾股定理求出![]() ,再由
,再由![]() ,
,![]() ,得出
,得出![]() ,然后由
,然后由![]() ,根据平行线分线段成比例定理得出
,根据平行线分线段成比例定理得出![]() ,列出比例式
,列出比例式![]() ,求解即可;
,求解即可;
(2)根据![]() ,即可得出
,即可得出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)根据四边形![]() 面积是
面积是![]() 面积的
面积的![]() ,列出方程
,列出方程![]() ,解方程即可;
,解方程即可;
(4)![]() 为等腰三角形时,分三种情况讨论:①
为等腰三角形时,分三种情况讨论:①![]() ;②
;②![]() ;③
;③![]() ,每一种情况都可以列出关于
,每一种情况都可以列出关于![]() 的方程,解方程即可.
的方程,解方程即可.
解:(1)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
解得![]() ;
;
(2)![]()
![]()
![]()
![]() ,
,
即![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() ;
;
(3)四边形![]() 面积能是
面积能是![]() 面积的
面积的![]() ,理由如下:
,理由如下:
由题意,得![]() ,
,
整理,得![]() ,
,
解得![]() ,
,![]() (不合题意舍去).
(不合题意舍去).
故四边形![]() 面积能是
面积能是![]() 面积的
面积的![]() ,此时
,此时![]() 的值为
的值为![]() ;
;
(4)![]() 为等腰三角形时,分三种情况讨论:
为等腰三角形时,分三种情况讨论:
①如果![]() ,那么
,那么![]() ,解得
,解得![]() ;
;
②如果![]() ,那么
,那么![]() ,解得
,解得![]() ;
;
③如果![]() ,那么
,那么![]() ,解得
,解得![]() .
.
故当![]() 为
为![]() 秒
秒![]() 秒
秒![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.
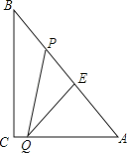

练习册系列答案
相关题目