题目内容
6. 实数a、b在数轴上的位置如图所示,则$\sqrt{{{(a+b)}^2}}$+$\sqrt{a^2}$的化简结果为-b.
实数a、b在数轴上的位置如图所示,则$\sqrt{{{(a+b)}^2}}$+$\sqrt{a^2}$的化简结果为-b.
分析 结合实数a、b在数轴上的位置,可判断出a>0,a+b<0,让后将$\sqrt{{{(a+b)}^2}}$+$\sqrt{a^2}$化简求解即可.
解答 解:结合实数a、b在数轴上的位置,可判断出a>0,a+b<0,
则有:$\sqrt{{{(a+b)}^2}}$+$\sqrt{a^2}$
=|a+b|+|a|
=-(a+b)+a
=-a-b+a
=-b.
故答案为:-b.
点评 本题考查了二次根式性质与化简,解答本题的关键在于结合实数a、b在数轴上的位置判断出a>0,a+b<0.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 已知△ABC,尺规作图.求作:
已知△ABC,尺规作图.求作: 如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.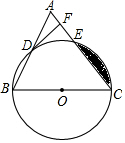 如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F.
如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F.