题目内容
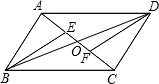如图，E、F是?ABCD的对角线AC上的两点，且CE=AF．请你猜想EF与BD能互相平分吗？并说明理由．考点：平行四边形的性质
专题：
分析：首先连接DE与BF，由四边形ABCD是平行四边变形，可得OA=OC，OB=OD，又由CE=AF，即可得OE=OF，继而证得四边形BEDF是平行四边形，则可证得EF与BD互相平分．
解答：
解：EF与BD互相平分．
理由：连接DE，BF，
∵四边形ABCD是平行四边变形，
∴OA=OC，OB=OD，
∵CE=AF，
∴AF-OA=CE-OC，
∴OE=OF，
∴四边形BEDF是平行四边形，
∴EF与BD互相平分．
解：EF与BD互相平分．理由：连接DE，BF，
∵四边形ABCD是平行四边变形，
∴OA=OC，OB=OD，
∵CE=AF，
∴AF-OA=CE-OC，
∴OE=OF，
∴四边形BEDF是平行四边形，
∴EF与BD互相平分．
点评：此题考查了平行四边形的性质与判定．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
用加减法解方程组
时，（1）-（2）得（ ）
|
| A、6x=-6 |
| B、2x=24 |
| C、2x=-6 |
| D、6x=24 |
某煤矿预计今年比去年增产15%，达到年产煤60万吨，设去年产煤x万吨，则可列方程（ ）
| A、x（1+15%）=60 |
| B、x（1-15%）=60 |
| C、60（1+15%）=x |
| D、x+15%=60 |
已知a＜0，b＞0，a+b＞0，则四个数a+b，|a+b|，|a|+b，a+|b|中，最大的是（ ）
| A、a+b | B、|a|+b |
| C、|a+b| | D、a+|b| |
用反证法证明命题“三角形的内角中至少有一个不大于60度”，应先假设（ ）
| A、三个内角都不大于60度 |
| B、三个内角都大于60度 |
| C、三个内角至多有一个大于60度 |
| D、假设三内角至多有一个不大于60度 |
如图一张长方形纸片沿AB折叠后，若∠1=70°，则∠2度数为（ ）| A、55° | B、35° |
| C、70° | D、40° |
方程2x-4=6的解是（ ）
| A、x=2 | B、x=3 |
| C、x=4 | D、x=5 |