题目内容
如图，△ABC≌△A′B′C，∠BCB′=40°，则∠ACA′=（ ）| A、30° | B、40° |
| C、120° | D、150° |
考点：全等三角形的性质
专题：
分析：根据全等三角形对应角相等可得∠ACB=∠A′CB′，再求出∠ACA′=∠BCB′．
解答：解：∵△ABC≌△A′B′C，
∴∠ACB=∠A′CB′，
∴∠ACB-∠ACB′=∠A′CB′-∠ACB′，
即∠ACA′=∠BCB′，
∵∠BCB′=40°，
∴∠ACA′=40°．
故选B．
∴∠ACB=∠A′CB′，
∴∠ACB-∠ACB′=∠A′CB′-∠ACB′，
即∠ACA′=∠BCB′，
∵∠BCB′=40°，
∴∠ACA′=40°．
故选B．
点评：本题考查了全等三角形的性质，熟记性质是解题的关键．
练习册系列答案
相关题目
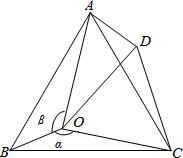如图所示，点O是等边△ABC内一点，∠BOC=α，∠AOB=β（α、β均不是锐角），将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．若△ABC≌△DEF，则下列结论错误的是（ ）
| A、BC=EF |
| B、∠B=∠D |
| C、∠C=∠F |
| D、AC=DF |