��Ŀ����
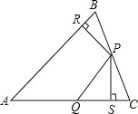
����Ŀ����֪����ͼ1��EΪBC�ӳ�����һ�㣮
��1����������ƽ����֤������ACE����ABC+��A��
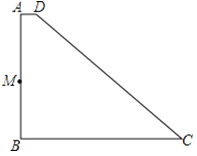
��2����ͼ2������D���߶�AC��һ�㣬��DF��BC����DGƽ�֡�BDF��AB��G��DHƽ�֡�GDC��BC��H���ҡ�BDC�ȡ�ACB��20�������GDH�Ķ�����
��3����ͼ3����֪EΪBC�ӳ�����һ�㣬D���߶�AC��һ�㣬����DE������ABC��ƽ�������ADE��ƽ�����ཻ�ڵ�P�������жϡ�P����A����E��������ϵ��֤����Ľ��ۣ�

���𰸡���1������������2��50������3����P��![]() ����A����E����������
����A����E����������
��������
��1������![]() ��
��![]() ��������ƽ���ߵ����ʽ��н���ɣ�
��������ƽ���ߵ����ʽ��н���ɣ�
��2������ƽ���ߵ����ʵ�![]() ���ٸ��ݽ�ƽ�������ʣ���
���ٸ��ݽ�ƽ�������ʣ���![]() ��ʾ
��ʾ![]() �����������ε��ڽǺͶ�����
�����������ε��ڽǺͶ�����![]() ��
��![]() ��
��![]() ��ϵ����
��ϵ����![]() ��ʾ
��ʾ![]() ����������
����������![]() ������ɽ�ƽ���ߵ����ʵý����
������ɽ�ƽ���ߵ����ʵý����
��3����![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ���������ε�������ʺͽ�ƽ���ߵ�֪ʶ��ɵó����ۣ�
���������ε�������ʺͽ�ƽ���ߵ�֪ʶ��ɵó����ۣ�
�⣺��1������![]() ��
��![]() ����ͼ1��
����ͼ1��

![]() ��
��![]() ��
��
![]() ��
��
��![]() ��
��
��2��![]() ��
��
![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
��3����![]() ��
��![]() �Ľ���Ϊ��
�Ľ���Ϊ��![]() ����ͼ2��
����ͼ2��

![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]()
![]() ��
��

��ϰ��ϵ�д�
�����Ŀ