题目内容
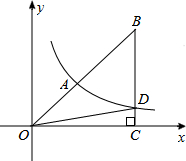如图，双曲线y=| k |
| x |
| AO |
| AB |
| 2 |
| 3 |
考点：反比例函数系数k的几何意义,相似三角形的判定与性质
专题：
分析：过A作AE⊥x轴于点E，根据反比例函数的比例系数k的几何意义可得S四边形AECB=S△BOD，根据△OAE∽△OBC，相似三角形面积的比等于相似比的平方，据此即可求得△OAE的面积，从而求得k的值．
解答：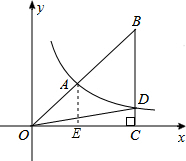
解：过A作AE⊥x轴于点E．
∵S△OAE=S△OCD，
∴S四边形AECB=S△BOD=21，
∵AE∥BC，
∴△OAE∽△OBC，
∴
=
=（
）2=
，
∴S△OAE=4，
则k=8．
故答案是：8．
解：过A作AE⊥x轴于点E．∵S△OAE=S△OCD，
∴S四边形AECB=S△BOD=21，
∵AE∥BC，
∴△OAE∽△OBC，
∴
| S△OAE |
| S△OBC |
| S△OAE |
| S△OAE+S四边形AECB |
| AO |
| OB |
| 4 |
| 25 |
∴S△OAE=4，
则k=8．
故答案是：8．
点评：本题考查反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．本知识点是中考的重要考点，同学们应高度关注．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
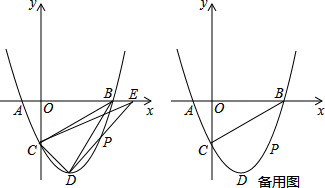
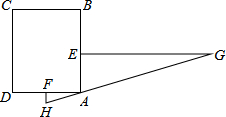“今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FH⊥AD，EG=15里，HG经过A点，则FH=