题目内容
 如图,矩形OABC和?ABEF,B(3,4).
如图,矩形OABC和?ABEF,B(3,4).(1)画出矩形OABC绕点O逆时针旋转90°后的矩形OA1B1C1,并写出B1的坐标为
(2)若点E的坐标为(5,2),则点F的坐标为
考点:作图-旋转变换
专题:
分析:(1)利用旋转的性质得出所画图形,进而得出B1的坐标,再利用弧长公式求出即可;
(2)利用平行四边形的性质以及中心对称图形的性质得出F点坐标以及直线l.
(2)利用平行四边形的性质以及中心对称图形的性质得出F点坐标以及直线l.
解答: 解:(1)如图所示:
解:(1)如图所示:
B1的坐标为:(-4,3),
∵B(3,4),
∴CO=4,BC=3,
∴BO=5,
∴点B运动到点 B1所经过的路径的长为:
=
;
故答案为:(-4,3),
;
(2)如图所示:直线l即为所求;
∵四边形ABEF是平行四边形,点E的坐标为(5,2),
∴AB=EF=4,则F(5,-2).
故答案为:(5,-2).
 解:(1)如图所示:
解:(1)如图所示:B1的坐标为:(-4,3),
∵B(3,4),
∴CO=4,BC=3,
∴BO=5,
∴点B运动到点 B1所经过的路径的长为:
| 90π×5 |
| 180 |
| 5π |
| 2 |
故答案为:(-4,3),
| 5π |
| 2 |
(2)如图所示:直线l即为所求;
∵四边形ABEF是平行四边形,点E的坐标为(5,2),
∴AB=EF=4,则F(5,-2).
故答案为:(5,-2).
点评:此题主要考查了旋转变换以及矩形和平行四边形的性质以及弧长公式等知识,得出对应点坐标是解题关键.

练习册系列答案
相关题目
武汉市一月份某周每天的最低气温是-2℃、-1℃、0℃、-1℃、1℃、2℃、3℃,那么这周的最低气温的最大差是( )
| A、-3℃ | B、2℃ |
| C、-5℃ | D、5℃ |
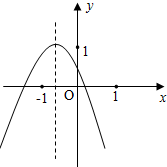 如图所示的是二次函数y=ax2+bx+c的图象,某学霸从下面五条信息中:
如图所示的是二次函数y=ax2+bx+c的图象,某学霸从下面五条信息中: 如图,下列是一个几何体的三视图,请确定这个几何体的形状.
如图,下列是一个几何体的三视图,请确定这个几何体的形状.