Question

【题目】如图，在矩形ABCD中，AB=18，AD=12，点M是边AB的中点，连结DM，DM与AC交于点G，点E，F分别是CD与DG上的点，连结EF，

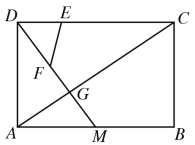
(1)求证：CG=2AG.

(2)若DE=6，当以E，F，D为顶点的三角形与△CDG相似时，求EF的长.

(3)若点E从点D出发，以每秒2个单位的速度向点C运动，点F从点G出发，以每秒1个单位的速度向点D运动.当一个点到达，另一个随即停止运动.在整个运动过程中，求四边形CEFG的面积的最小值.

Answer 1

【答案】(1)证明见解析；(2) EF=；(3)S四边形CEFG最小=52.

【解析】

(1)利用矩形的性质及平行线的性质，可证得∠DCG=∠MAG，,∠CDG=∠AMG，△AGM∽△CGD，再利用相似三角形的对应边相等，可得比例线段，然后证明DC=AB=2AM，即可证得CG与AG的数量关系.

(2)利用勾股定理，分别求出AC、DG的长，再分情况讨论：①当∠DEF=∠DCG时，△DEF∽△DCG；②当∠DEF=∠DGC时，△DEF∽△DGC，分别利用相似三角形的性质，得出对应边成比例，即可求出EF的长.

(3)作GH⊥DC，FN⊥DC，易证△DNF∽△MAD，可证对应边成比例，求出NF的长，再根据S四边形CEFG=S△DCG-S△DEF，可得到S与t的函数解析式，再利用二次函数的性质，可求出四边形CEFG的面积的最小值.

证明：(1)在矩形ABCD中，AB∥DC,

∴∠DCG=∠MAG,∠CDG=∠AMG,

∴△AGM∽△CGD,

∴

∵点M是边AB的中点,

∴DC=AB=2AM,

∴=2，CG即CG=2AG

(2)在Rt△ADC中,由勾股定理得AC=,

由(1)得CG=2AG，CG=AC=4，同理可得DG=10

①当∠DEF=∠DCG时,△DEF∽△DCG

∴ 即 ,解得EF=

②当∠DEF=∠DGC时,△DEF∽△DGC

∴ ,即 ,解得EF=

(3)作GH⊥DC,FN⊥DC,

设运动时间为t，则DF=DG-FG=10-t，DE=2t，

∵∠DNF=∠DAM,∠NDF=∠AMD,

∴△DNF∽△MAD

∴ 即 ，解得NF=

∵S四边形CEFG=S△DCG-S△DEF

∴当t=5时，S四边形CEFG最小=52