Question

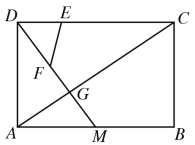
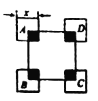
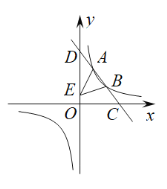
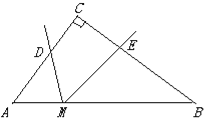
【题目】如图，在Rt△ABC中，已知AC=3，BC=4，点M是AB边上的一个动点，∠DME的两边与折线A—C—B分别交于点D和点E(点E在点D的右边)，且∠DME=∠A，若能使以点D，E，M为顶点的三角形与△ABC相似的点D有三个，则AM的长度x的取值范围是________.

Answer 1

【答案】或

【解析】

当CM⊥AB于点M，DM⊥AC于点D时，此时点C，E重合，根据已知条件易证△DCM∽△CAB∽△ACM，利用相似三角形的对应边成比例，可求出x的值，即可得到x的取值范围；如图，当点M为AB的中点，ME⊥BC于点E，点C、D重合，利用直角三角形斜边的性质，可求出AM的长，同理可得到点D的另一个点，综上所述，可得到x的取值范围.

如图，CM⊥AB于点M，DM⊥AC于点D，此时点C，E重合，

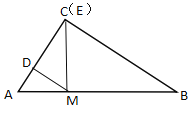
∴∠CDM=∠ACB=∠AMC=90°，

∴∠DMC+∠ADM=90°，∠ADM+∠A=90°，

∴∠A=∠DME

∴△DCM∽△CAB∽△ACM，

∴

在Rt△ABC中，

∴

解得，

∴0＜x＜；

如图，当点M为AB的中点，ME⊥BC于点E，点C、D重合.

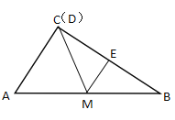
∵BC⊥AC

∴ME∥AC

∴∠CME=∠ACM

∵CM是Rt△ABC的中线，

∴CM=AM=BM= ，

∴∠A=∠ACM=∠CME

∴x=；

同理可得到点D的另一个点，此时

∴x的取值范围为 <x<

故答案为：或