Question

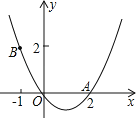
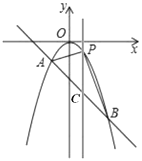
【题目】如图所示，已知抛物线与一次函数的图象相交于，两点，点是抛物线上不与，重合的一个动点.

（1）请求出，，的值；

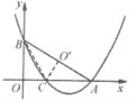
（2）当点在直线上方时，过点作轴的平行线交直线于点，设点的横坐标为，的长度为，求出关于的解析式；

（3）在（2）的基础上，设面积为，求出关于的解析式，并求出当取何值时，取最大值，最大值是多少？

Answer 1

【答案】（1），，；（2）；（3）当时，取最大值，最大值为

【解析】

（1）把A、B坐标分别代入抛物线和一次函数解析式即可求出a、b、k的值；（2）根据a、b、k的值可得抛物线和直线AB的解析式，根据P点横坐标为m可用m表示P、C两点坐标，根据两点间距离公式即可得L与m的关系式；（3）如图，作AD⊥PC于D，BE⊥PC于E，根据，可用m表示出S，配方求出二次函数的最值即可得答案.

（1）∵点A（-1，-1）在抛物线图象上，

∴，

解得：，

∵点A（-1，-1）、B（2，-4）在一次函数的图象上，

∴，

解得，

∴，，

（2）∵，，a=-1，

∴直线的解析式为，抛物线的解析式为，

∵点P在抛物线上，点C在直线AB上，点P横坐标为m，PC//y轴，

∴，，

∴关于的解析式：，

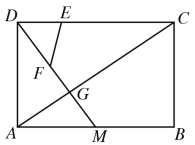
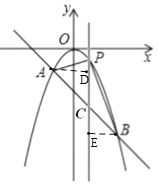
（3）如图，作AD⊥PC于D，BE⊥PC于E，

∴AD=m+1，BE=2-m，

∵，

∴PC·AD+PC·BE

配方得：，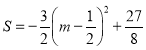

∴当时，取最大值，最大值为