题目内容
19.有五张正面分别标有数字-2、-1、0、1、2的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x的方程x2-4x-2a+2=0的两根均为正数的概率为$\frac{2}{5}$.分析 分别把5个数代入方程,然后解方程可确定一元二次方程x2-4x-2a+2=0的根均为正数的a的值,再利用概率公式求解.
解答 解:当a=-2时,方程变形为x2-4x+6=0,△=16-4×1×6<0,方程没有实数解;
当a=-1时,方程变形为x2-4x+4=0,两根相等为2;
当a=0时,方程变形为x2-4x+2=0,解得x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$;
当a=1时,方程变形为x2-4x=0,两根为0或4;
当a=2时,方程变形为x2-4x-2=0,解得x1=2+$\sqrt{6}$,x2=2-$\sqrt{6}$,
所以从中任取一张,将该卡片上的数字记为a,则使关于x的方程x2-4x-2a+2=0的两根均为正数的概率=$\frac{2}{5}$
故答案为$\frac{2}{5}$
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
9.下列说法正确的是( )
| A. | 数字0也是单项式 | B. | -x2的系数是1 | ||
| C. | -2πx2的系数是-2 | D. | x2+1是二次单项式 |
10.为增强居民的节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准如下:
李磊家11月份用电200度,缴纳电费136元,则x=0.6.超出部分电费单价是1.
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过160度的部分 | x |
| 超过160度的部分 | x+0.4 |
11.在Rt△ABC中,如果∠C=90°,AB=10,BC=8,那么cosB的值是( )
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |

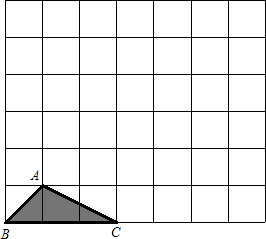 按要求完成作图.
按要求完成作图.