题目内容
16．已知二次函数y=x2-4x-12的图象与x轴交于点A，B，则AB的长为8．分析 首先令y=0，解得A，B两点的横坐标，根据横坐标即可得AB的长．
解答 解：令y=0得：0=x2-4x-12，
解得：x1=6，x2=-2，
∴AB的长度为：6-（-2）=8，
故答案为8．
点评 本题考查了抛物线和x轴的交点问题，求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．
练习册系列答案
相关题目
11．
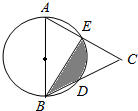如图，AB是⊙O的直径，点D、E是半圆的三等分点，AE、BD的延长线交于点C．若CE=3，则图中由线段BD，BE和弧DE围成的阴影部分的面积是（ ）
如图，AB是⊙O的直径，点D、E是半圆的三等分点，AE、BD的延长线交于点C．若CE=3，则图中由线段BD，BE和弧DE围成的阴影部分的面积是（ ）| A． | $\frac{4}{3}$π-$\sqrt{3}$ | B． | $\frac{3}{2}π$ | C． | $\frac{2}{3}$π-$\sqrt{3}$ | D． | $\frac{8}{3}π$ |
如图，△OCA≌△OBD，则这两个三角形中相等的边有AC=BD，OC=OB，OA=OD，相等的角有∠A=∠D，∠C=∠B，∠AOC=∠DOB．
如图，已知?ABCD中，DE⊥AC，BF⊥AC，证明：四边形DEBF为平行四边形．