Question

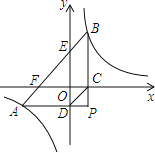
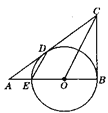
【题目】如图1，CB、CD是⊙O的切线，切点分别为B、D，CD的延长线与⊙O的直径BE的延长线交于A点，连OC，ED．

（1）探索OC与ED的位置关系，并加以证明；

（2）若OD=4，CD=6，求tan∠ADE的值．

Answer 1

【答案】（1）OC//ED，证明见详解；（2）tan∠ADE=．

【解析】

(1)连接OD，证明△COD△COB，则∠COD =∠COB；又∠DOB是等腰三角形ODE的外角，则∠DOB= 2∠DEB，由此可证得∠COB =∠DEB；同位角相等，则DE//OC；

(2)Rt△A BC中，由勾股定理易求得AB的长；然后在Rt△ADO中，用⊙O的半径表示出OA的长，再根据勾股定理求出⊙O的半径，则Rt△COD中，即可求得∠OCD的正切值，由(1)知：∠ADE=∠OCE，由此可求出∠ADE的正切值．

解：(1)OC//ED ，

证明：连接OD；BC，CD是⊙O的切线，

∴∠CBO=∠CDO= 90°，

∵OD= OB，CO= CO，

∴△COB △COD，

∴∠COD=∠COB，

又∵OD= OE，

∴∠EDO=∠DEO，

∴∠DEO=∠DOB，

∴∠DEO=∠COB，

∴OC// ED．

(2)∵CD=6，AD= 4，

∴CB= 6,AC= 10，

∴AB = 8，

设⊙O的半径为r,

在Rt△ADO中有

解得r= 3，

∵OC// ED，

∴∠ADE=∠DCO，

在Rt△COD中， tan∠DCO = ，

∴tan∠ADE=．