题目内容
如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.
(1)当CD=1时,求点E的坐标;
(2)如果设CD=t,梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由.

 (1)证明:∵CD、CB是⊙O的切线,
(1)证明:∵CD、CB是⊙O的切线,
∴∠ODC=∠OBC=90°
又∵ OD=OB,OC=OC,
∴△OBC≌△ODC(HL)
(2)选择a、b、c,或其中2个均给分;
方法一:在Rt△EBC中,由勾股定理:
(b+2r)2+c2=(a+c)2,得r=![]() .
.
方法二:Rt△ODE∽Rt△CBE,![]() ,得r=
,得r=![]() .
.
方法三:连结AD,可证:AD//OC,![]() ,得r=
,得r=![]() .
.
若选择a、c:需综合运用以上的多种方法,得r=![]() .
.
若选择b、c,则有关系式2r3+br2-bc2=0.
(以上解法仅供参考,只要解法正确均给分)
25,解:(1) 正方形OABC中,因为ED⊥OD,即∠ODE =90°
所以∠CDO+∠EDB=90°,即∠COD=90°-∠CDO,而 ∠EDB =90°-∠CDO,
所以∠COD =∠EDB 又因为∠OCD=∠DBE=90°
所以△CDO∽△BED,
所以![]() ,即
,即![]() ,得BE=
,得BE=![]() ,
,
则:![]()
因此点E的坐标为(4,![]() ).
).
(2) 存在S的最大值.
由△CDO∽△BED,
所以![]() ,即
,即![]() ,BE=t-
,BE=t-![]() t2,
t2,
![]() ×4×(4+t-
×4×(4+t-![]() t2)
t2)![]() .
.
故当t=2时,S有最大值10.
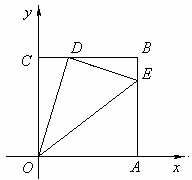

练习册系列答案
相关题目

 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
