题目内容
如图,⊙O的半径OA与OB互相垂直,P是线段OB延长线上的一点,连接AP交⊙O于点D,点E在OP上且DE=EP.(1)求证:DE是⊙O的切线;
(2)作DH⊥OP于点H,若HE=6,DE=4
 ,求⊙O的半径的长.
,求⊙O的半径的长.
【答案】分析:(1)利用等腰三角形的性质首先得出∠2=∠P,∠A=∠1,再利用∠A+∠P=90°,得出∠1+∠2=90°即可得出OD⊥DE,即可证出;
(2)首先利用cos∠3= =
= 即可求出∠3=30°,再利用在Rt△ODE中,tan∠3=
即可求出∠3=30°,再利用在Rt△ODE中,tan∠3= ,即可求出⊙O的半径OD.
,即可求出⊙O的半径OD.
解答: (1)证明:连接OD.
(1)证明:连接OD.
∵OA=OD,
∴∠A=∠1.
∵DE=EP,
∴∠2=∠P.
∵OA⊥OB于O,
∴∠A+∠P=90°.
∴∠1+∠2=90°.
∴∠ODE=90°.
即 OD⊥DE.
∵OD是⊙O的半径,
∴DE是⊙O的切线.
(2)解:∵DH⊥OP于点H,
∴∠DHE=90°.
∵HE=6,DE=4 ,
,
∴cos∠3= =
= =
= .
.
∴∠3=30°
∵在Rt△ODE中,tan∠3= ,
,
∴ =
= .
.
∴OD=4.
即⊙O的半径为4.
点评:此题主要考查了圆的综合应用以及切线的判定和锐角三角函数应用,利用等腰三角形的性质得出∠2=∠P,∠A=∠1是解题关键.
(2)首先利用cos∠3=
 =
= 即可求出∠3=30°,再利用在Rt△ODE中,tan∠3=
即可求出∠3=30°,再利用在Rt△ODE中,tan∠3= ,即可求出⊙O的半径OD.
,即可求出⊙O的半径OD.解答:
 (1)证明:连接OD.
(1)证明:连接OD.∵OA=OD,
∴∠A=∠1.
∵DE=EP,
∴∠2=∠P.
∵OA⊥OB于O,
∴∠A+∠P=90°.
∴∠1+∠2=90°.
∴∠ODE=90°.
即 OD⊥DE.
∵OD是⊙O的半径,
∴DE是⊙O的切线.
(2)解:∵DH⊥OP于点H,
∴∠DHE=90°.
∵HE=6,DE=4
 ,
,∴cos∠3=
 =
= =
= .
.∴∠3=30°
∵在Rt△ODE中,tan∠3=
 ,
,∴
 =
= .
.∴OD=4.
即⊙O的半径为4.
点评:此题主要考查了圆的综合应用以及切线的判定和锐角三角函数应用,利用等腰三角形的性质得出∠2=∠P,∠A=∠1是解题关键.

练习册系列答案
相关题目
 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )
如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )| A、10 | B、8 | C、6 | D、4 |
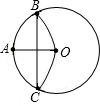 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )A、6
| ||
B、6
| ||
C、3
| ||
D、3
|
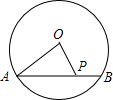 如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为
如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为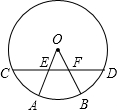 如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.
如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.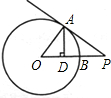 如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,
如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,