题目内容
|a|=1,|b|=2,|c|=3,且a>b>c,则a+b-c=
- A.-2
- B.0
- C.2或0
- D.4
C
分析:首先根据绝对值确定a,b,c的可能数值,然后根据a>b>c,即可确定a,b,c的值,从而求解.
解答:由|a|=1知,a=±1,又因为a>b>c,故b=-2,c=-3,则
①当a=1时,a+b-c=1+(-2)-(-3)=2;
②当a=-1时,a+b-c=-1+(-2)-(-3)=0.
故答案是0或2.
故选C.
点评:本题主要考查了绝对值的性质,若|x|=a(a>0),则x=a或-a.正确确定a,b,c的值是解决本题的关键.
分析:首先根据绝对值确定a,b,c的可能数值,然后根据a>b>c,即可确定a,b,c的值,从而求解.
解答:由|a|=1知,a=±1,又因为a>b>c,故b=-2,c=-3,则
①当a=1时,a+b-c=1+(-2)-(-3)=2;
②当a=-1时,a+b-c=-1+(-2)-(-3)=0.
故答案是0或2.
故选C.
点评:本题主要考查了绝对值的性质,若|x|=a(a>0),则x=a或-a.正确确定a,b,c的值是解决本题的关键.

练习册系列答案
相关题目
 如图,∠AOB放置在正方形网格中,则cos∠AOB的值为
如图,∠AOB放置在正方形网格中,则cos∠AOB的值为


 如图所示是一个中空的正方体,它的俯视图是
如图所示是一个中空的正方体,它的俯视图是



 去分母,得
去分母,得 大小判断正确的是
大小判断正确的是



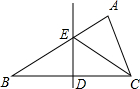 △ABC中,BC的中垂线交AB于E、交BC于D,BC=10,△BCE的周长为22,则BE=________.
△ABC中,BC的中垂线交AB于E、交BC于D,BC=10,△BCE的周长为22,则BE=________. 若一个几何体的三视图如下图所示:则这个几何体是
若一个几何体的三视图如下图所示:则这个几何体是 的和是
的和是


