题目内容
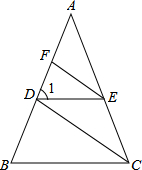 如图,CD,EF分别平分∠ACB,∠AED,CD∥EF,D,F在AB上,∠1=∠AED,则∠B与∠ACB相等吗?为什么?
如图,CD,EF分别平分∠ACB,∠AED,CD∥EF,D,F在AB上,∠1=∠AED,则∠B与∠ACB相等吗?为什么?考点:平行线的判定与性质
专题:
分析:根据平行线的性质和角平分线的性质得到∠AED=∠ACB,则DE∥BC,由该平行线的性质得到∠AED=∠ACB,∠1=∠B.又∠1=∠AED,则易证得结论.
解答:解: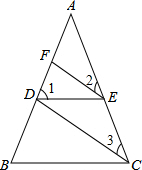 ∠B与∠ACB相等.理由如下:
∠B与∠ACB相等.理由如下:
∵CD∥EF,
∴∠2=∠3.
又CD,EF分别平分∠ACB,∠AED,
∴∠AED=2∠2,∠ACB=2∠3,
∴∠AEC=∠ACB,
∴DE∥BC,
∴∠AED=∠ACB,∠1=∠B.
又∠1=∠AED,
∴∠B=∠ACB,即∠B与∠ACB相等.
 ∠B与∠ACB相等.理由如下:
∠B与∠ACB相等.理由如下:∵CD∥EF,
∴∠2=∠3.
又CD,EF分别平分∠ACB,∠AED,
∴∠AED=2∠2,∠ACB=2∠3,
∴∠AEC=∠ACB,
∴DE∥BC,
∴∠AED=∠ACB,∠1=∠B.
又∠1=∠AED,
∴∠B=∠ACB,即∠B与∠ACB相等.
点评:本题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
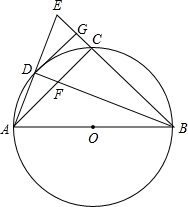 如图,AB是⊙O的直径,点C为弧AB的中点,∠ABC的角平分线交⊙O于点D,交AC于点F,AD、BC的延长线交于点E,DG⊥BE于点G.
如图,AB是⊙O的直径,点C为弧AB的中点,∠ABC的角平分线交⊙O于点D,交AC于点F,AD、BC的延长线交于点E,DG⊥BE于点G.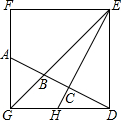 如图,DEFG为正方形,A、H分别是FG、GD的中点,DA分别与GE、HE相交于B、C,则AB:BC:CD=
如图,DEFG为正方形,A、H分别是FG、GD的中点,DA分别与GE、HE相交于B、C,则AB:BC:CD=