题目内容
平面直角坐标系中,过点A(1,2)作直线l与x轴正半轴、y轴正半轴分别交于B、C点,若△BOC(O为坐标原点)的面积为4,则这样的直线有
- A.0条
- B.1条
- C.2条
- D.3条
B
分析:直线的解析式是y=kx+b,把A(1,2)代入得到b=2-k,推出y=kx+2-k,分别求出当x=0,y=0时,对应的y、x的值,求出OB、OC,根据三角形的面积公式求出即可.
解答: 解:设直线的解析式是y=kx+b,
解:设直线的解析式是y=kx+b,
把A(1,2)代入得:2=k+b,
∴b=2-k,
∴y=kx+2-k,
当x=0时,y=2-k,
当y=0时,x=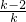 ,
,
OB=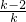 ,OC=k-2,
,OC=k-2,
∵△BOC(O为坐标原点)的面积为4,
∴ OB×OC=4,
OB×OC=4,
即 ×
×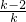 ×(2-k)=4,
×(2-k)=4,
解得:k=-2,
∴直线的解析式是y=-2x+4,
故选B.
点评:本题主要考查对一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,解一元二次方程,三角形的面积等知识点的理解和掌握,能推出 ×
×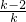 ×(2-k)=4是解此题的关键.
×(2-k)=4是解此题的关键.
分析:直线的解析式是y=kx+b,把A(1,2)代入得到b=2-k,推出y=kx+2-k,分别求出当x=0,y=0时,对应的y、x的值,求出OB、OC,根据三角形的面积公式求出即可.
解答:
 解:设直线的解析式是y=kx+b,
解:设直线的解析式是y=kx+b,把A(1,2)代入得:2=k+b,
∴b=2-k,
∴y=kx+2-k,
当x=0时,y=2-k,
当y=0时,x=
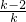 ,
,OB=
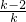 ,OC=k-2,
,OC=k-2,∵△BOC(O为坐标原点)的面积为4,
∴
 OB×OC=4,
OB×OC=4,即
 ×
×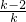 ×(2-k)=4,
×(2-k)=4,解得:k=-2,
∴直线的解析式是y=-2x+4,
故选B.
点评:本题主要考查对一次函数图象上点的坐标特征,用待定系数法求一次函数的解析式,解一元二次方程,三角形的面积等知识点的理解和掌握,能推出
 ×
×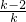 ×(2-k)=4是解此题的关键.
×(2-k)=4是解此题的关键. 
练习册系列答案
相关题目
 21、在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
21、在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
 (2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是
(2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是 在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.
在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长与面积相等,则点P是和谐点.