题目内容
若x+y=m+n,且x2+y2=m2+n2.求证:x2001+y2001=m2001+n2001.分析:首先根据题干条件x+y=m+n,且x2+y2=m2+n2,求出|x-y|=|m-n|,然后求出x、y和m、n之间的关系,即可证明出等式成立.
解答:解:∵x+y=m+n…①,
x2+y2=m2+n2…②,
①平方-②得:(x+y)2-(x2+y2)=(m+n)2-(m2+n2),
∵x2+y2=m2+n2,
∴原式可化为:(x+y)2-(m2+n2)=(m+n)2-(m2+n2),即(x-y)2=(m-n)2,
|x-y|=|m-n|,
分别与x+y=m-n联立,
解得
或
,
都有x2001+y2001=m2001+n2001.
综上等式证明.
x2+y2=m2+n2…②,
①平方-②得:(x+y)2-(x2+y2)=(m+n)2-(m2+n2),
∵x2+y2=m2+n2,
∴原式可化为:(x+y)2-(m2+n2)=(m+n)2-(m2+n2),即(x-y)2=(m-n)2,
|x-y|=|m-n|,
分别与x+y=m-n联立,
解得
|
|
都有x2001+y2001=m2001+n2001.
综上等式证明.
点评:本题主要考查分式的等式证明的知识点,证明出x、y和m、n之间的关系是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
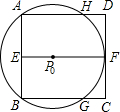 装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
 (2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为
(2013•丰台区一模)如图,在平面直角坐标系xOy中,⊙C的圆心坐标为(-2,-2),半径为 C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.