Question

一块直角三角形形状的铁皮材料，两直角边长分别为30cm、40cm，现要把它加工成一个面积最大的正方形，两种加工方法如图①、②，请你用学过的知识说明哪种加工方法符合要求？

Answer 1

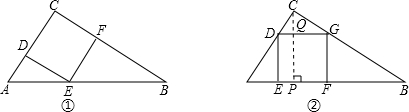
分析：在图①中设正方形的边长为x，则DE=x，AD=30-x，由相似三角形的判定定理得出△ADE∽△ACB，根据相似三角形的对应边成比例即可求出x的值；在图②中过点C作CP⊥AB，垂足为P，CP交DG于Q．由三角形的面积公式求出CP的长度，
由相似三角形的判定定理得出△CDG∽△CAB，设DG=y，根据相似三角形的对应边成比例求出y的长度，比较出x，y的大小即可得出结论．

解答：解：在图①中设正方形的边长为x，则DE=x，AD=30-x
∵∠A=∠A，∠ADE=∠C=90°
∴△ADE∽△ACB，
∴

AD

AC

=

DE

BC

，即

30-x

30

=

x

40

，
解得x=

120

7

．
在图②中过点C作CP⊥AB，垂足为P，CP交DG于Q．
∵S_△ABC=

1

2

AC•BC=

1

2

AB•CP，
∴CP=

AC•BC

AB

=

30×40

50

=24．
∵DG∥AB，
∴∠CDG=∠A，∠CGD=∠B，
∴△CDG∽△CAB，
∴

DG

AB

=

CQ

CP

．
设DG=y，

y

50

=

24-y

24

，
解得y=

120

7.4

．
∵

120

7.4

＜

120

7

，
∴y＜x．
∴图①方法符合要求．

点评：本题考查的是相似三角形在实际生活中的运用，此类题目有利于培养学生理论联系实际的能力．