题目内容
19. 如图,△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠DAE=12°.求∠C的度数.
如图,△ABC中,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠DAE=12°.求∠C的度数.
分析 根据垂直得出∠ADC=∠ADB=90°,根据三角形内角和定理求出∠BAE,根据角平分线定义求出∠CAE=∠BAE=38°,求出∠CAD=26°,根据三角形内角和定理的求出即可.
解答 解:∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵∠B=40°,∠DAE=12°,
∴∠BAE=90°-∠B-∠DAE=38°,
∵AE平分∠BAC,
∴∠CAE=∠BAE=38°,
∵∠DAE=12°,
∴∠CAD=38°-12°=26°,
∵∠ADC=90°,
∴∠C=90°-∠CAD=64°.
点评 本题考查了三角形内角和定理,垂直定义,角平分线定义的应用,能运用定理求出各个角的度数是解此题的关键,注意:三角形的内角和等于180°.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.在如图的△ABC中,正确画出AC边上的高的图形是( )
| A. |  | B. |  | C. |  | D. |  |
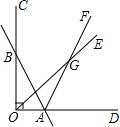 已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.