题目内容
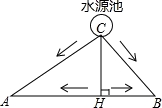
如图所示,A、B两块试验田相距200米,C为水源地,AC=160m,BC=120m,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断△ABC的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
【考点】勾股定理的应用.
【分析】(1)由勾股定理的逆定理即可得出△ABC是直角三角形;
(2)由△ABC的面积求出CH,得出AC+BC<CH+AH+BH,即可得出结果.
【解答】解:(1)△ABC是直角三角形;理由如下:
∴AC2+BC2=1602+1202=40000,AB2=2002=40000,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)甲方案所修的水渠较短;理由如下:
∵△ABC是直角三角形,
∴△ABC的面积= AB•CH=
AB•CH= AC•BC,
AC•BC,
∴CH= =
= =96(m),
=96(m),
∵CH⊥AB,
∴∠AHC=90°,
∴AH= =
= =128(m),
=128(m),
∴BH=AB﹣AH=72m,
∵AC+BC=160m+120m=280m,CH+AH+BH=96m+200m=296m,
∴AC+BC<CH+AH+BH,
∴甲方案所修的水渠较短.
【点评】本题考查了勾股定理的应用、勾股定理的逆定理、三角形面积的计算;熟练掌握勾股定理,由勾股定理的逆定理证出△ABC是直角三角形是解决问题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
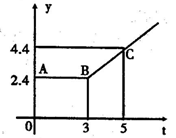
小学生10分钟应用题系列答案某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数。(如下表)
| 每人加工零件数 | 540 | 450 | 300 | 240 | 210 | 120 |
| 人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1) 写出这15人该月加工零件数的平均数.中位数和众数;
(2) 假设生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理?
| 成绩 | 划记 | 频数 | 百分比 |
| 不及格 |
| 9 | 10% |
| 及格 | 正正正 | 18 | 20% |
| 良好 | 正正正正正正正¯ | 36 | 40% |
| 优秀 | 正正正正正Т | 27 | 30% |
| 合计 | 90 | 90 | 100% |
 正
正
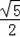
 ,如果Rt△ABC的面积为1,则它的周长为( )
,如果Rt△ABC的面积为1,则它的周长为( )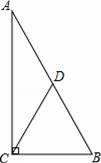

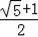
 B.
B.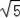
 +1 C.
+1 C.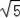

 ﹣
﹣

 ,其中x为方程x2+x﹣3=0的根.
,其中x为方程x2+x﹣3=0的根.