题目内容
16. 如图,?ABCD (AB<AD)的纸片的对角线AC与BD相交于点O,将这张纸片对折后点B与点D重合,点A落在点E,已知∠AOB=α,那么∠CEO的度数为90°-α.
如图,?ABCD (AB<AD)的纸片的对角线AC与BD相交于点O,将这张纸片对折后点B与点D重合,点A落在点E,已知∠AOB=α,那么∠CEO的度数为90°-α.
分析 先画出图形,由折叠的性质证明△OEF≌△OCF,继而可得△OEF是直角三角形,∠OFE=90°,根据∠AOB=α,可求∠CEO的度数.
解答 解:如图所示: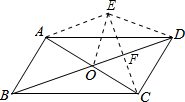
由折叠的性质可得:∠AOB=∠EOF=∠COF,OE=OA=OC,
在△OEF和△OCF中,
$\left\{\begin{array}{l}{OE=OC}\\{∠EOF=∠COF}\\{OF=OF}\end{array}\right.$,
∴△OEF≌△OCF(SAS),
∴∠OFE=∠OFC=90°,
∵∠AOB=α,
∴∠EOF=α,
∴∠CEO=90°-α.
故答案为:90°-α.
点评 本题考查了翻折变换的性质以及平行四边形的性质,解决问题的关键是掌握:翻折前后对应边相等、对应角相等,解题时注意:平行四边形的对角线互相平分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.计算2sin45°的结果等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
6.已知菱形的周长为40,一条对角线长为12,则这个菱形的面积为( )
| A. | 40 | B. | 47 | C. | 96 | D. | 190 |