��Ŀ����
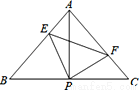
��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ���AE=CF�� �ڡ�EPFһ���ǵ���ֱ�������Σ� ��S�ı���AEPF=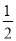 S��ABC���ܵ���EPF�ڡ�ABC���ƶ���P��תʱʼ����EF=AP������E����A��B�غϣ�������������ʼ����ȷ����_____.��д��ţ�
S��ABC���ܵ���EPF�ڡ�ABC���ƶ���P��תʱʼ����EF=AP������E����A��B�غϣ�������������ʼ����ȷ����_____.��д��ţ�
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ


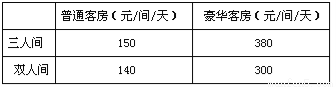
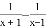 ���ɵã� ��
���ɵã� ��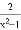 B.
B. 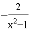 C.
C. 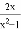 D.
D. 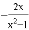
 ��ʵ��ʱ����_________��
��ʵ��ʱ����_________��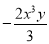 ��ϵ����
��ϵ���� 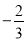 �������� 4
�������� 4