题目内容
18.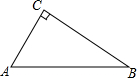 已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为3<r≤4或r=$\frac{12}{5}$.
已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为3<r≤4或r=$\frac{12}{5}$.
分析 根据直线与圆的位置关系得出相切时有一交点,再结合图形得出另一种有一个交点的情况,即可得出答案.
解答 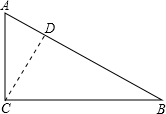 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
∵AC=3,BC=4.如果以点C为圆心,r为半径的圆与斜边AB只有一个公共点,
∴AB=5,
当直线与圆相切时,d=r,圆与斜边AB只有一个公共点,圆与斜边AB只有一个公共点,
∴CD×AB=AC×BC,
∴CD=r=$\frac{12}{5}$,
当直线与圆如图所示也可以有一个交点,
∴3<r≤4,
故答案为:3<r≤4或r=$\frac{12}{5}$.
点评 此题主要考查了直线与圆的位置关系,结合题意画出符合题意的图形,从而得出答案,此题比较容易漏解.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
8.反比例函数y=-$\frac{3}{x}$的图象在坐标系的( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二象限 | D. | 第三、四象限 |
13.若关于x,y的二元一次方程组mx+ny=0的解是x=5,y=-1,已知m<0,则关于x的不等式(m+n)x>n-m的解集是( )
| A. | x<-$\frac{2}{3}$ | B. | x>-$\frac{2}{3}$ | C. | x<$\frac{2}{3}$ | D. | x>$\frac{2}{3}$ |
3.下列说法错误的是( )
| A. | 频率等于频数与组距比值 | |
| B. | 在频数分布直方图中,频数之和为数据个数 | |
| C. | 在频数分布表中,频率之和为1 | |
| D. | 频率等于频数与样本容量的比值 |