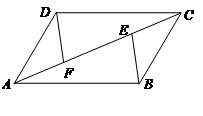题目内容
已知:如图,梯形ABCD中,AD∥BC,∠B=90°,AD= ,BC=
,BC= ,DC=
,DC= ,
,
且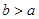 ,点M是AB边的中点.
,点M是AB边的中点.
(1)求证:CM⊥DM;
(2)求点M到CD边的距离.(用含 ,
, 的式子表示)
的式子表示)
 ,BC=
,BC= ,DC=
,DC= ,
,且
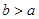 ,点M是AB边的中点.
,点M是AB边的中点.(1)求证:CM⊥DM;
(2)求点M到CD边的距离.(用含
 ,
, 的式子表示)
的式子表示)
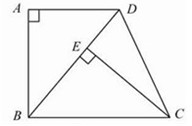
证明:(1)延长DM,CB交于点E.(如图3)
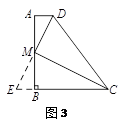
∵梯形ABCD中,AD∥BC,
∴∠ADM=∠BEM.
∵点M是AB边的中点,
∴AM=BM.
在△ADM与△BEM中,
 ∠ADM=∠BEM,
∠ADM=∠BEM,
∠AMD=∠BME,
AM=BM,
∴△ADM≌△BEM.
∴AD=BE= ,DM=EM.
,DM=EM.
∴CE=CB+BE=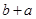 .
.
∵CD=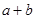 ,
,
∴CE=CD.
∴CM⊥DM.
解:(2)分别作MN⊥DC,DF⊥BC,垂足分别为点N,F.(如图4)
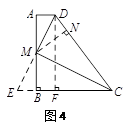
∵CE=CD,DM=EM,
∴CM平分∠ECD.
∵∠ABC= 90°,即MB⊥BC,
∴MN=MB.
∵AD∥BC,∠ABC=90°,
∴∠A=90°.
∵∠DFB=90°,
∴四边形ABFD为矩形.
∴BF= AD= ,AB= DF.
,AB= DF.
∴FC= BC-BF =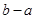 .
.
∵Rt△DFC中,∠DFC=90°,
∴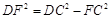 =
=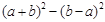 =
=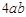 .
.
∴ DF=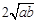 .
.
∴MN=MB=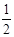 AB=
AB=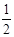 DF=
DF=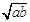 .
.
即点M到CD边的距离为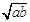 .
.

∵梯形ABCD中,AD∥BC,
∴∠ADM=∠BEM.
∵点M是AB边的中点,
∴AM=BM.
在△ADM与△BEM中,
 ∠ADM=∠BEM,
∠ADM=∠BEM,∠AMD=∠BME,
AM=BM,
∴△ADM≌△BEM.
∴AD=BE=
 ,DM=EM.
,DM=EM.∴CE=CB+BE=
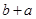 .
.∵CD=
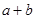 ,
,∴CE=CD.
∴CM⊥DM.
解:(2)分别作MN⊥DC,DF⊥BC,垂足分别为点N,F.(如图4)

∵CE=CD,DM=EM,
∴CM平分∠ECD.
∵∠ABC= 90°,即MB⊥BC,
∴MN=MB.
∵AD∥BC,∠ABC=90°,
∴∠A=90°.
∵∠DFB=90°,
∴四边形ABFD为矩形.
∴BF= AD=
 ,AB= DF.
,AB= DF. ∴FC= BC-BF =
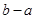 .
. ∵Rt△DFC中,∠DFC=90°,
∴
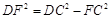 =
=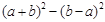 =
=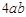 .
.∴ DF=
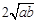 .
. ∴MN=MB=
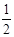 AB=
AB=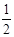 DF=
DF=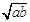 .
.即点M到CD边的距离为
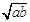 .
. (1)等腰三角形三线合一,证得CE=CD,即可得CM⊥DM;
(2)构建直角三角形利用勾股定理求解。
(2)构建直角三角形利用勾股定理求解。

练习册系列答案
相关题目

 方格中,每个小正方形的边长都是
方格中,每个小正方形的边长都是 ,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.
,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.
 的梯形;
的梯形;




 是四边形
是四边形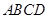 的对角线
的对角线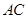 上两点,
上两点,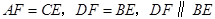 .
. ;
;