题目内容
如图，已知AO是△ABC的∠A的平分线，BD⊥AO的延长线于D，E是BC的中点．
求证：DE=
（AB-AC）
证明：延长AC、BD交于点F，∵在△ABD和△AFD中，
，∴△ABD≌△AFD（ASA），
∴AB=AF，BD=DF，
又∵E是BC的中点，即ED是△BCF中位线，
∴DE=
CF=（AB-AC）．分析：延长AC、BD交于点F，可以证得△ABF是等腰三角形，则DE是△BCF的中位线，依据三角形中位线定理即可证得．
点评：本题考查了三角形的中位线定理，以及等腰三角形的性质，正确证得DE是△BCF中位线是关键．
练习册系列答案
同步练习强化拓展系列答案
相关题目
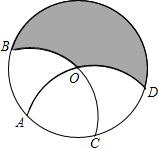如图，已知A是半径为1的⊙O上一点，以A为圆心，AO为半径画弧交⊙O于点B、C；以C为圆心，CO为半径画弧交⊙O于点D、A，则图中阴影面积为
（2013•宁德质检）如图，已知BC是⊙O的直径，AB是⊙O的切线，AO交⊙O于点D，∠A=28°，则∠C=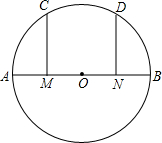
如图，已知AB是⊙O的直径，M，N分别是AO，BO的中点，CM⊥AB，DN⊥AB．求证：
如图，已知AO是△ABC的∠A的平分线，BD⊥AO的延长线于D，E是BC的中点．