Question

12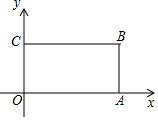．在平面直角坐标系中，A（4，0）、B（4，2）、C（0，2）．直线y=kx-k+3（k是常数）将四边形OABC分成面积相等的两部分，则k的值是-2．

Answer 1

分析 由条件可先求得矩形OABC的中心坐标，再由直线分矩形面积相等的两部分可知直线过矩形的中心，代入可求得k的值．

解答 解：如图，连接OB、AC交于点D，过D作DE⊥x轴，过D作DF⊥y轴，垂足分别为E、F，

∵A（4，0），B（4，2），C（0，2），
∴四边形OABC为矩形，
∴DE=$\frac{1}{2}$OA=$\frac{1}{2}$×4=2，DF=$\frac{1}{2}$OC=$\frac{1}{2}$×2=1，
∴D（2，1），
∵直线y=kx-k+3（k是常数）将四边形OABC分成面积相等的两部分，
∴直线过点D，
则2k-k+3=1，
解得：k=-2，
故答案为：-2．

点评 本题主要考查矩形的判定和性质，掌握过矩形中心的直线平分矩形面积是解题的关键．