题目内容
(1)如图1,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是
(2)如图2,一副三角板叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0<α<180),当△ACD的一边与△AOB的某一边平行时,相应的旋转角α的值是 .
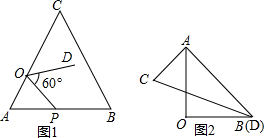
(2)如图2,一副三角板叠放在一起,若固定△AOB,将△ACD绕着公共顶点A,按顺时针方向旋转α度(0<α<180),当△ACD的一边与△AOB的某一边平行时,相应的旋转角α的值是

考点:旋转的性质
专题:计算题
分析:(1)根据等边三角形的性质得到∠A=∠C=60°,由AC=9,OA=3得OC=6,再根据旋转的性质得OD=OP,∠DOP=60°,然后证明△AOP≌△CDO,所以AP=OC=6;
(2)根据旋转的定义旋转角为∠BAD,分类讨论:当CD∥AB时,如图①;当AC∥OB时,如图②;当CD∥OA时,如图③;当AD∥OB时,如图④;当CD∥OB时,如图⑤,然后根据平行线的性质和旋转的性质求∠DAB的度数.
(2)根据旋转的定义旋转角为∠BAD,分类讨论:当CD∥AB时,如图①;当AC∥OB时,如图②;当CD∥OA时,如图③;当AD∥OB时,如图④;当CD∥OB时,如图⑤,然后根据平行线的性质和旋转的性质求∠DAB的度数.
解答:(1)解:如图1,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵AC=9,OA=3,
∴OC=6,
∵线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上
∴OD=OP,∠DOP=60°,
∴∠AOP+∠COD=120°,
而∠AOP+∠APO=120°,
∴∠COD=∠APO,
在△AOP和△CDO中
,
∴△AOP≌△CDO(AAS),
∴AP=OC=6.
故答案为6;
(2)在△AOB中,∠AOB=90°,∠OAB=∠OBA=45°;在△ACD中,∠CAD=90°,∠ACD=60°,∠ADC=30°,
当CD∥AB时,如图①,∠BAD=∠ADC=30°,旋转角为∠BAD,所以α=30°;
当AC∥OB时,如图②,∠CAD=∠BOA=90°,AD与OA共线,
旋转角为∠DAB,所以α=45°;
当CD∥OA时,如图③,∠ADC=∠OAD=30°,则∠DAB=∠OAD+∠OAB=30°+45°=75°,旋转角为∠DAB,所以α=75°;
当AD∥OB时,如图④,∠DAO=∠BOA=90°,∠ADB=∠DAO+∠OAB=135°,旋转角为∠DAB,所以α=135°;
当CD∥OB时,如图⑤,延长OA交CD于E,则∠DEA=∠AOB=90°,而∠D=30°,所以∠DAE=60°,∠DAO=120°,所以∠DAB=120°+45°=165°,
旋转角为∠DAB,所以α=165°,
综上所述,旋转角α的值为30°,45°,75°,135°,165°.
故答案为30°,45°,75°,135°,165°.

∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵AC=9,OA=3,
∴OC=6,
∵线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上
∴OD=OP,∠DOP=60°,
∴∠AOP+∠COD=120°,
而∠AOP+∠APO=120°,
∴∠COD=∠APO,
在△AOP和△CDO中
|
∴△AOP≌△CDO(AAS),
∴AP=OC=6.

故答案为6;
(2)在△AOB中,∠AOB=90°,∠OAB=∠OBA=45°;在△ACD中,∠CAD=90°,∠ACD=60°,∠ADC=30°,
当CD∥AB时,如图①,∠BAD=∠ADC=30°,旋转角为∠BAD,所以α=30°;
当AC∥OB时,如图②,∠CAD=∠BOA=90°,AD与OA共线,
旋转角为∠DAB,所以α=45°;
当CD∥OA时,如图③,∠ADC=∠OAD=30°,则∠DAB=∠OAD+∠OAB=30°+45°=75°,旋转角为∠DAB,所以α=75°;
当AD∥OB时,如图④,∠DAO=∠BOA=90°,∠ADB=∠DAO+∠OAB=135°,旋转角为∠DAB,所以α=135°;
当CD∥OB时,如图⑤,延长OA交CD于E,则∠DEA=∠AOB=90°,而∠D=30°,所以∠DAE=60°,∠DAO=120°,所以∠DAB=120°+45°=165°,
旋转角为∠DAB,所以α=165°,
综上所述,旋转角α的值为30°,45°,75°,135°,165°.
故答案为30°,45°,75°,135°,165°.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质和平行线的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如果关于x的不等式组
无解,那么m的取值范围是( )
|
| A、m>1 | B、m≥1 |
| C、m<1 | D、m≤1 |
不等式6x<4x-1的解集是( )
A、x>
| ||
B、x>-
| ||
C、x<-
| ||
D、x<
|

 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C(0,2),点M(m,n)是抛物线上一动点,位于对称轴的左侧,并且不在坐标轴上,过点M作x轴的平行线交y轴于点Q,交抛物线于另一点E,直线BM交y轴于点F.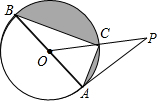 如图,△ABC内接于⊙O,AB为⊙O的直径,∠BAC=2∠B,AC=6,过点A作⊙O的切线与OC的延长线交于P.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠BAC=2∠B,AC=6,过点A作⊙O的切线与OC的延长线交于P.