题目内容
16.四张不透明的卡片A、B、C、D,正面分别画有等边三角形、矩形和等腰梯形、平行四边形,除正面画有不同的图形外,其它都相同,把这四张卡片洗匀后,正面向下放在桌上.
(1)从这四张卡片中任意摸出一张,求卡片上的图形是中心对称图形但不是轴对称图形的概率;
(2)从这四张卡片中任意摸出一张不放回,再从中任意摸出一张,请用列表法或画树状图的方法,求两次抽取的卡片证明图形都是中心对称图形的概率.
分析 (1)找出四张卡片中是中心对称图形但不是轴对称图形的情况数,即可求出所求的概率;
(2)列表得出所有等可能的情况数,找出两次都为中心对称图形的情况数,即可求出所求的概率.
解答 解:(1)从四张卡片中任意摸出一张,卡片上的图形是中心对称图形但不是轴对称图形的概率为$\frac{1}{4}$;
(2)列表如下:
| A | B | C | D | |
| A | --- | (B,A) | (C,A) | (D,A) |
| B | (A,B) | --- | (C,B) | (D,B) |
| C | (A,C) | (B,C) | --- | (D,C) |
| D | (A,D) | (B,D) | (C,D) | --- |
则两次都为中心对称图形的概率为$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6.在0,-2.5,2,-3这四个数中,最小的数是( )
| A. | 2 | B. | -3 | C. | -2.5 | D. | 0 |
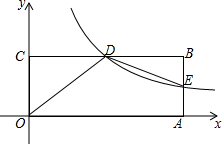 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=$\frac{4}{3}$. 如图,△ABC的顶点都在正方形网格的格点上,则tanA=1.
如图,△ABC的顶点都在正方形网格的格点上,则tanA=1.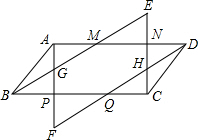 如图,四边形ABCD是平行四边形,AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点.
如图,四边形ABCD是平行四边形,AF∥CE,BE∥DF,AF交BE于G点,交DF于F点,CE交DF于H点、交BE于E点. 已知等边△ABC,以AC为腰,在△ABC外作等腰三角形,AD=AC,连接BD,则∠BDC=30°度.
已知等边△ABC,以AC为腰,在△ABC外作等腰三角形,AD=AC,连接BD,则∠BDC=30°度.