题目内容
 在△AOB中,AB=OB=2,△COD中,CD=OC=3,∠ABO=∠DCO.连接AD、BC,点M、N、P分别为OA、OD、BC的中点.
在△AOB中,AB=OB=2,△COD中,CD=OC=3,∠ABO=∠DCO.连接AD、BC,点M、N、P分别为OA、OD、BC的中点.①若A、O、C三点在同一直线上,且∠ABO=2α,则
| AD | BC |
②固定△AOB,将△COD绕点O旋转,PM最大值为
分析:(1)连接BM、CN,则BM⊥OA,CN⊥OD,由四点共圆的判定知点B、C、M、N在以BC为直径的圆,且有MP=PN=BC÷2,而MN是△AOD的中位线,有MN等于AD的一半,故AD:BC=MN:PM,而可求得△PMN∽△BAO,有MN:PN=AO:AB=2sinα,从而求得AD:BC的值;
(2)当DC∥AB时,即四边形ABCO是梯形时,PM有最大值,由梯形的中位线的公式可求解.
(2)当DC∥AB时,即四边形ABCO是梯形时,PM有最大值,由梯形的中位线的公式可求解.
解答: 解:连接BM、CN,
解:连接BM、CN,
由题意知BM⊥OA,CN⊥OD,∠AOB=∠COD=90°-α,
∵A、O、C三点在同一直线上,
∴B、O、D三点也在同一直线上,
∴∠BMC=∠CNB=90°,
∵P为BC中点,
∴在Rt△BMC中,PM=
BC,在Rt△BNC中,PN=
BC,
∴PM=PN,
∴B、C、N、M四点都在以点P为圆心,
BC为半径的圆上,
∴∠MPN=2∠MBN,
又∵∠MBN=
∠ABO=α,
∴∠MPN=∠ABO,
∴△PMN∽△BAO,
∴
=
,
由题意知MN=
AD,PM=
BC,
∴
=
,
∴
=
,
在Rt△BMA中,
=sinα,
∵AO=2AM,
∴
=2sinα,
∴
=2sinα;
(2)当DC∥AB时,即四边形ABCO是梯形时,PM有最大值.
PM=(AB+CD)÷2=(2+3)÷2=
.
 解:连接BM、CN,
解:连接BM、CN,由题意知BM⊥OA,CN⊥OD,∠AOB=∠COD=90°-α,
∵A、O、C三点在同一直线上,
∴B、O、D三点也在同一直线上,
∴∠BMC=∠CNB=90°,
∵P为BC中点,
∴在Rt△BMC中,PM=
| 1 |
| 2 |
| 1 |
| 2 |
∴PM=PN,
∴B、C、N、M四点都在以点P为圆心,
| 1 |
| 2 |
∴∠MPN=2∠MBN,
又∵∠MBN=
| 1 |
| 2 |
∴∠MPN=∠ABO,
∴△PMN∽△BAO,
∴
| MN |
| PM |
| AO |
| BA |
由题意知MN=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AD |
| BC |
| MN |
| PM |
∴
| AD |
| BC |
| AO |
| BA |
在Rt△BMA中,
| AM |
| AB |
∵AO=2AM,
∴
| AO |
| BA |
∴
| AD |
| BC |
(2)当DC∥AB时,即四边形ABCO是梯形时,PM有最大值.
PM=(AB+CD)÷2=(2+3)÷2=
| 5 |
| 2 |
点评:本题利用了相似三角形的性质和等腰三角形的性质:三线合一、四点共圆的判定、正弦的概念、梯形的中位线的性质求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
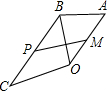 已知:如图,在△AOB中,AB=2,C为平面内一点,且OC=3,线段OC绕点O旋转一周,连接BC,M、P分别为OA、BC的中点,则在OC旋转的过程中PM的范围为( )
已知:如图,在△AOB中,AB=2,C为平面内一点,且OC=3,线段OC绕点O旋转一周,连接BC,M、P分别为OA、BC的中点,则在OC旋转的过程中PM的范围为( )| A、2<PM<3 | B、1<PM≤2.5 | C、0.5≤PM<3 | D、0.5≤PM≤2.5 |
 已知:在△AOB中,AB=
已知:在△AOB中,AB= = (用含有α的式子表示);
= (用含有α的式子表示);
 = (用含有α的式子表示);
= (用含有α的式子表示);