题目内容
3．
如图，在△ABC中，E是BC上一点，EC=2BE，点D是AC的中点，若S△ABC=15，则S△ADF-S△BEF=2.5．
分析 根据题意先分别求出S△ABD，S△ABE，再根据S△ADF-S△BEF=S△ABD-S△ABE即可求出结果．
解答 解：∵点D是AC的中点，
∴AD=$\frac{1}{2}$AC，
∵S△ABC=15，
∴S△ABD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×15=7.5．
∵EC=2BE，S△ABC=15，
∴S△ABE=$\frac{1}{3}$S△ABC=$\frac{1}{3}$×15=5，
∵S△ABD-S△ABE=（S△ADF+S△ABF）-（S△ABF+S△BEF）=S△ADF-S△BEF，
即S△ADF-S△BEF=S△ABD-S△ABE=7.5-5=2.5．
故答案为：2.5．
点评 本题考查三角形的面积的计算方法；关键知道当高相等时，面积等于底边的比，根据此可求出三角形的面积，然后求出差．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
13．已知点A（a，1）与点B（5，b）是关于原点O的对称点，则（ ）
| A． | a=-5，b=-1 | B． | a=-5，b=1 | C． | a=5，b=-1 | D． | a=5，b=1 |
已知：如图，在△ABC中，∠C=90°，MN是BC的中垂线，将△ABC绕点A按顺时针方向旋转，使点C落在直线MN上的点C1，得到△AB1C1，联结BC1，如果∠CAC1=24°，求∠CBC1的大小．
11．下列说法正确的是（ ）
| A． | 平方是本身的数是0 | B． | 立方等于本身的数是1、-1 | ||
| C． | 绝对值是本身的数是正数 | D． | 倒数是本身的数是1、-1 |
18．下列说法正确的是（ ）
| A． | 全等三角形的三条边相等，三个角也相等 | |
| B． | 判定两个三角形全等的条件中至少有一个是等边 | |
| C． | 面积相等的两个图形是全等形 | |
| D． | 全等三角形的面积和周长都相等 |
8．已知点A（-1，y1）、B（2，y2）都在双曲线y=$\frac{3+2m}{x}$上，则y1、y2的大小关系是（ ）
| A． | y1＜y2 | B． | y1＞y2 | C． | y1=y2 | D． | 无法确定 |
如图，六边形ABCDEF为⊙O的内接正六边形，AC、AE交BF于M、N两点，求证：
12．等式$\frac{3x+1}{4}$-1=2x的下列变形属于等式性质2的变形是（ ）
| A． | $\frac{3x+1}{4}$=2x+1 | B． | $\frac{3x+1}{4}$-2x=1 | C． | 3x+1-4=8x | D． | $\frac{3}{4}$x+$\frac{1}{4}$-1=2x |
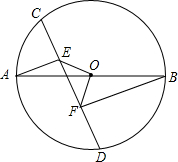如图：在⊙O中，AB是直径，CD是弦，$\widehat{AD}$=$\widehat{BD}$，过点A、B两点分别作CD的垂线，垂足分别是点E、F．连接OE，OF，求证：△OEF是等腰直角三角形．